Trong không gian cho điểm A và ba mặt phẳng đôi một vuông góc (P1), (P2) và (P3) giao nhau tại O. Gọi A1, A2, A3 lần lượt là hình chiếu vuông góc của A trên các mặt phẳng (P1), (P2) và (P3). Gọi M, N, P lần lượt là chân đường vuông góc hạ từ A xuống các giao tuyến của (P1) và (P2), (P2) và (P3), (P3) và (P1).
a) Chứng minh OA2 = OM2 + ON2 + OP2.
b) Áp dụng ý a để chứng minh \(OA = \sqrt {\frac{{OA_1^2 + OA_2^2 + OA_3^2}}{2}} \).
Sử dụng kết quả trên để tính độ dài của một đoạn thẳng mà ba hình chiếu có độ dài lần lượt là 1 cm, 2 cm và 3 cm.
Trong không gian cho điểm A và ba mặt phẳng đôi một vuông góc (P1), (P2) và (P3) giao nhau tại O. Gọi A1, A2, A3 lần lượt là hình chiếu vuông góc của A trên các mặt phẳng (P1), (P2) và (P3). Gọi M, N, P lần lượt là chân đường vuông góc hạ từ A xuống các giao tuyến của (P1) và (P2), (P2) và (P3), (P3) và (P1).
a) Chứng minh OA2 = OM2 + ON2 + OP2.
b) Áp dụng ý a để chứng minh \(OA = \sqrt {\frac{{OA_1^2 + OA_2^2 + OA_3^2}}{2}} \).
Sử dụng kết quả trên để tính độ dài của một đoạn thẳng mà ba hình chiếu có độ dài lần lượt là 1 cm, 2 cm và 3 cm.
Câu hỏi trong đề: Chuyên đề Toán 11 KNTT Bài tập cuối chuyên đề 3 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải:
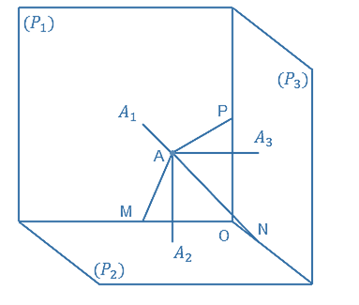
a) Áp dụng định lí Pythagore cho các tam giác vuông.
Tam giác OMA vuông tại M có: OA2 = OM2 + AM2 (1)
Tam giác ONA vuông tại N có: OA2 = ON2 + AN2 (2)
Tam giác OPA vuông tại P có: OA2 = OP2 + AP2 (3)
Cộng vế theo vế của (1), (2), (3) ta được:
3OA2 = (OM2 + ON2 + OP2) + (AM2 + AN2 + AP2)
Ta chứng minh được: AM2 + AN2 + AP2 = 2OA2. (4)
Suy ra: OA2 = OM2 + ON2 + OP2.
b) Vì AM vuông góc OM, OM // AA3 nên AM vuông góc AA3
Mà AA3 vuông góc với OA3
Suy ra: AM // OA3 và AA3 // OM nên AMOA3 là hình bình hành.
Do đó: AM = OA3.
Chứng minh tương tự ta được: AN = OA1, AP = OA2.
Thay kết quả trên vào (4) ta được: \(OA_3^2 + OA_2^2 + OA_1^2 = 2O{A_2}\).
Suy ra \(OA = \sqrt {\frac{{OA_1^2 + OA_2^2 + OA_3^2}}{2}} \).
Ba hình chiếu có độ dài lần lượt là 1 cm, 2 cm và 3 cm.
Thay số vào kết quả trên ta được: \(OA = \sqrt {\frac{{{1^2} + {2^2} + {3^2}}}{2}} = \sqrt 7 \) (cm).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Lời giải:
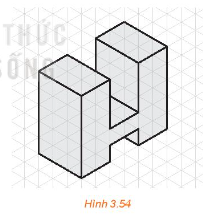
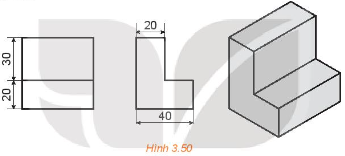
Bước 1: Nhận thấy rằng vật thể có dạng khối chữ H được bao bởi một hình hộp chữ nhật, hai phần rãnh cũng là hình hộp chữ nhật.
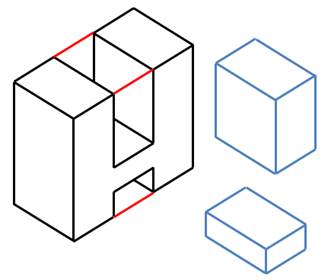
Bước 2: Chọn các hướng chiếu lần lượt vuông góc với mặt trước, mặt trên và mặt bên trái của vật thể.
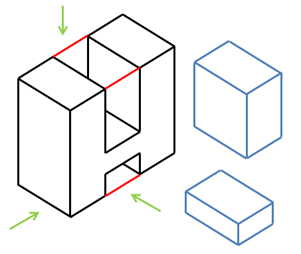
Bước 3: Lần lượt vẽ hình chiếu vuông góc của hình hộp chữ nhật bao bên ngoài vật thể, của khối chữ H và của rãnh hộp chữ nhật.
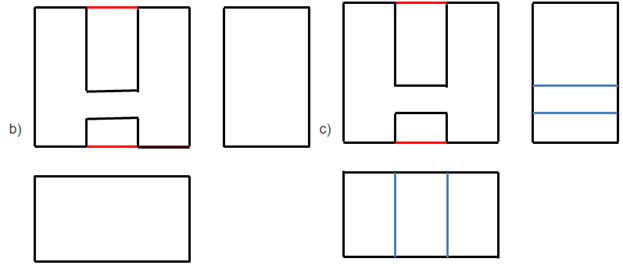
Bước 4: Xóa các nét thừa, chỉnh sửa các nét vẽ theo quy tắc: các đường thấy vẽ bằng nét liền; các đường khuất vẽ bằng nét đứt. Ghi các kích thước của vật thể trên các hình chiếu.
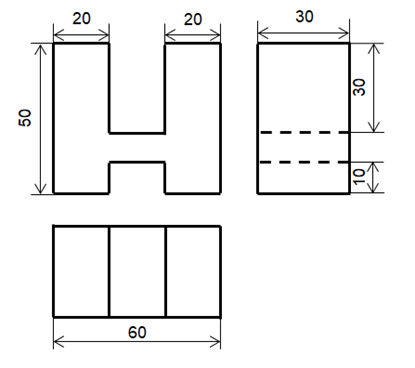
Bước 5: Vẽ hình chiếu trục đo vuông góc đều của vật thể.
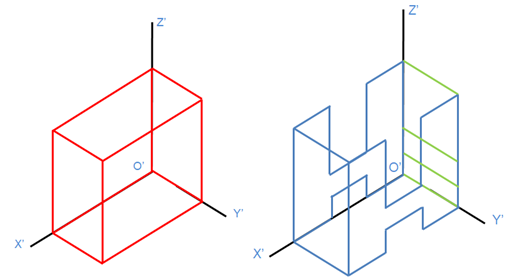
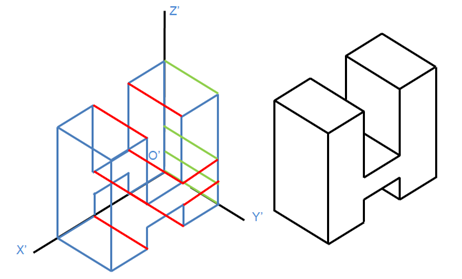
Bước 6: Hoàn thành khung tên, khung bản vẽ để được bản vẽ cuối cùng có dạng như sau:
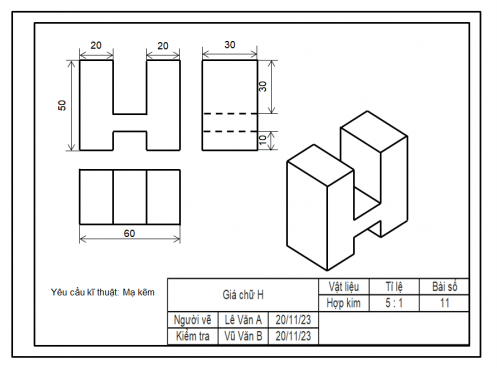
Ta có: Thể tích của giá chữ H bằng hiệu thể tích của hình hộp chữ nhật bao ngoài và thể tích của hai rãnh hộp chữ nhật.
Thể tích hình hộp chữ nhật bao ngoài là: 60 . 30 . 50 = 90 000 (mm3).
Thể tích rãnh hộp chữ nhật thứ nhất là: 30 . 20 . 30 = 18 000 (mm3).
Thể tích rãnh hộp chữ nhật thứ hai là: 20 . 30 . 10 = 6 000 (mm3).
Vậy thể tích của giá chữ H là: 90 000 – 18 000 – 6 000 = 66 000 (mm3).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Lời giải:
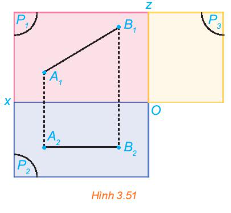
a) Hình chiếu cạnh của đoạn thẳng AB có hai đầu mút là hình chiếu cạnh A3 của A và B3 của B.
Để xác định A3 ta làm như sau: Qua điểm A2 vẽ đường thẳng vuông góc với Oz tại C và trên tia đối của tia Ox lấy điểm D sao cho OC = OD. Đường thẳng qua A1 và vuông góc với Oz cắt đường thẳng qua D và vuông góc với Ox tại A3. Tương tự xác định B3. Nối A3 và B3 ta nhận được hình chiếu cạnh của đoạn thẳng AB.
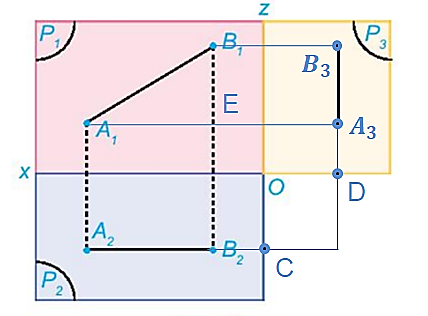
b) Gọi E là giao điểm của A1A3 và B1B2.
Dễ dàng chứng minh tứ giác A1A2B2E là hình chữ nhật.
Do đó: A1E = A2B2.
Mà A2B2 = 6 cm nên A1E = 6 cm.
Tam giác A1B1E vuông tại E nên A1E2 + B1E2 = A1B12 (định lí Pythagore)
Suy ra \({B_1}E = \sqrt {{A_1}{B_1}^2 - {A_1}{E^2}} = \sqrt {{{10}^2} - {6^2}} = 8\) (cm).
Mà B1E = A3B3 (A3B3B1E là hình chữ nhật)
Vậy A3B3 = 8 cm.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập