Rút gọn biểu thức:A=x−2xxx−1+x+1xx+x+x+1+2x−2xx2−x (x > 0, x khác 1)

=xx−1x+2xx−1x+x+1 Vậy A=x+2x+x+1.

Câu hỏi:

02/08/2023 265

Rút gọn biểu thức: $A = \frac{x - 2 \sqrt{x}}{x \sqrt{x} - 1} + \frac{\sqrt{x} + 1}{x \sqrt{x} + x + \sqrt{x}} + \frac{1 + 2 x - 2 \sqrt{x}}{x^{2} - \sqrt{x}}$ (x > 0, x khác 1)

Xem lời giải

Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

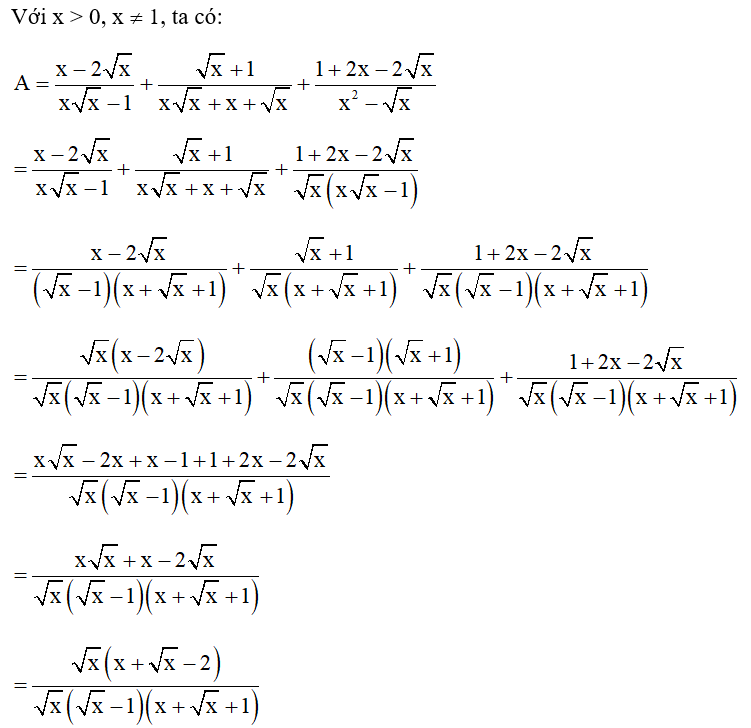
Rút gọn biểu thức: A= x - 2 căn x/ x căn x - 1 + căn x +1/ x căn x + x + căn x + 1 + 2 x - 2 căn x/ x^2 - căn x (x > 0, x khác 1) (ảnh 1)

= \frac{\sqrt{x} (\sqrt{x} - 1) (\sqrt{x} + 2)}{\sqrt{x} (\sqrt{x} - 1) (x + \sqrt{x} + 1)}

Vậy $A = \frac{\sqrt{x} + 2}{x + \sqrt{x} + 1}$ .

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một thí sinh tham gia kì thi THPT Quốc gia. Trong bài thi môn Toán bạn đó làm được chắc chắn đúng 40 câu. Trong 10 câu còn lại chỉ có 3 câu bạn loại trừ được mỗi câu một đáp án chắc chắn sai. Do không còn đủ thời gian nên bạn bắt buộc phải khoanh bừa các câu còn lại. Hỏi xác suất bạn đó được 9 điểm là bao nhiêu?

Xem đáp án

Lời giải

Bài thi có 50 câu nên mỗi câu đúng được 0,5 điểm. Như vậy để được 9 điểm, thí sinh

này phải trả lời đúng thêm 5 câu nữa.

Trong 10 câu còn lại chia làm 2 nhóm:

* Nhóm A là 3 câu đã loại trừ được một đáp án chắc chắn sai.

Nên xác suất chọn được phương án trả lời đúng là $\frac{1}{3}$ , xác suất chọn được phương án trả lời sai là $\frac{2}{3}$ .

* Nhóm B là 7 câu còn lại, xác suất chọn được phương án trả lời đúng là $\frac{1}{4}$ , xác suất chọn được phương án trả lời sai là $\frac{3}{4}$ .

Ta có các trường hợp sau:

• Trường hợp 1: Có 3 câu trả lời đúng thuộc nhóm A và 2 câu trả lời đúng thuộc nhóm B.

Xác xuất là $P_{1} = {(\frac{1}{3})}^{3} . C_{7}^{2} . {(\frac{1}{4})}^{2} . {(\frac{3}{4})}^{5} = \frac{189}{16384}$

• Trường hợp 2: Có 2 câu trả lời đúng thuộc nhóm A và 3 câu trả lời đúng thuộc nhóm B.

Xác xuất là $P_{2} = C_{3}^{2} {(\frac{1}{3})}^{2} . \frac{2}{3} . C_{7}^{3} . {(\frac{1}{4})}^{3} . {(\frac{3}{4})}^{4} = \frac{315}{8 192}$ .

• Trường hợp 3: Có 1 câu trả lời đúng thuộc nhóm A và 4 câu trả lời đúng thuộc nhóm B.

Xác xuất là $P_{3} = C_{3}^{1} \cdot \frac{1}{3} \cdot {(\frac{2}{3})}^{2} \cdot C_{7}^{4} \cdot {(\frac{1}{4})}^{4} \cdot {(\frac{3}{4})}^{3} = \frac{105}{4 096}$

• Trường hợp 4: Không có câu trả lời đúng nào thuộc nhóm A và 5 câu trả lời đúng thuộc nhóm B.

Xác xuất là $P_{4} = {(\frac{2}{3})}^{3} \cdot C_{7}^{5} \cdot {(\frac{1}{4})}^{5} \cdot {(\frac{3}{4})}^{2} = \frac{7}{2 048}$ .

Xác suất cần tìm là: $P = P_{1} + P_{2} + P_{3} + P_{4} = \frac{1 295}{16 384} = 0,079$ .

Vậy xác suất bạn đó được 9 điểm là 0,079.

Câu 2

Trong kỳ thi THPT Quốc Gia năm 2016 có môn thi bắt buộc là môn Tiếng Anh. Môn thi này thi dưới hình thức trắc nghiệm với 4 phương án trả lời A, B, C, D. Mỗi câu trả lời đúng được cộng 0,2 điểm và mỗi câu trả lời sai bị trừ đi 0,1 điểm. Bạn Hoa vì học rất kém môn Tiếng Anh nên chọn ngẫu nhiên cả 50 câu trả lời. Tính xác xuất để bạn Hoa đạt được 4 điểm môn Tiếng Anh trong kỳ thi trên.

Xem đáp án

Lời giải

Gọi x là số câu trả lời đúng, suy ra 50 − x là số câu trả lời sai.

Ta có số điểm của Hoa là 0,2 . x − 0,1 . (50 − x) = 4 ⇔ x = 30 .

Do đó bạn Hoa trả lời đúng 30 câu và sai 20 câu.

Không gian mẫu là số phương án trả lời 50 câu hỏi mà bạn Hoa chọn ngẫu nhiên. Mỗi câu có 4 phương án trả lời nên có 450 khả năng.

Suy ra số phần tử của không gian mẫu là | Ω | = 450.

Gọi X là biến cố "Bạn Hoa trả lời đúng 30 câu và sai 20 câu".

Vì mỗi câu đúng có 1 phương án trả lời, mỗi câu sai có 3 phương án trả lời.

Vì vậy có $C_{50}^{30}$ . (3)20 khả năng thuận lợi cho biến cố X.

Suy ra số phần tử của biến cố X là | Ω X | = $C_{50}^{30}$ . (3)20.

Xác suất cần tính $P (X) = \frac{| Ω X |}{| Ω |} = \frac{C_{50}^{30} . {(3)}^{20}}{4^{50}}$ .

Vậy xác suất để bạn Hoa đạt được 4 điểm môn Tiếng Anh trong kỳ thi trên là $\frac{C_{50}^{30} . {(3)}^{20}}{4^{50}}$ .

Câu 3