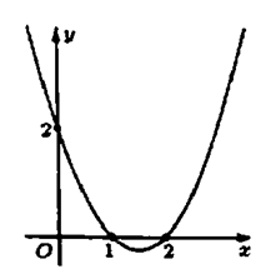
Cho hàm số y = f(x) có đạo hàm f '(x) trên R. Hình vẽ bên là đồ thị của hàm số y = f '(x). Hàm số g(x) = f(x − x2) nghịch biến trên khoảng nào trong các khoảng dưới đây:
A. ;
B. ;
C. ;
D. .
Cho hàm số y = f(x) có đạo hàm f '(x) trên R. Hình vẽ bên là đồ thị của hàm số y = f '(x). Hàm số g(x) = f(x − x2) nghịch biến trên khoảng nào trong các khoảng dưới đây:

A. ;
B. ;
C. ;
D. .
Quảng cáo
Trả lời:
Đáp án đúng là: C
Ta có: g' (x) = (1 – 2x)f '(x – x2)
Hàm số y = g(x) nghịch biến trên (a; b)
Û g' (x) ≤ 0 "x Î (a; b) và bằng 0 tạ hữu hạn điểm
Ta có: g' (1) = 3f '(–2) > 0
Do đó loại đáp án A, B, D ta chọn đáp án C.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
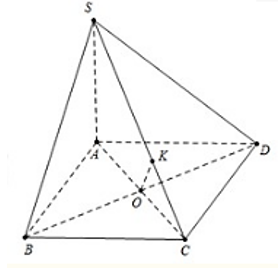
Gọi O là tâm hình vuông ABCD
Ta có: AC ^ BD; BD ^ SA
Do đó BD ^ (SAC)
Dựng OK ^ SC
Do đó OK là đoạn vuông góc chung của BD và SC
Khi đó (1)
Ta có: AC2 = AB2 + BC2 = 2a2
Suy ra
Thay vào (1) ta có .
Vậy .
Lời giải
Trong tam giác vuông CDA:
Trong tam giác vuông CDB:
AB = BD – AD = 116,7 – 25,7 = 91 (m).
Vậy khoảng cách AB là 91 m.Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.