Cho đường thẳng d1: y = mx + 2m – 1 ( với m là tham số) và d2: y = x + 1. a) Với m = 2. Hãy vẽ các đường thẳng d1 và d2 trên cùng 1 mặt phẳng tọa độ . Tìm tọa độ giao điểm của 2 đường thẳng d1 và d2....

Câu hỏi:

19/08/2025 4,955

Cho đường thẳng d₁: y = mx + 2m – 1 ( với m là tham số) và d₂: y = x + 1.

a) Với m = 2. Hãy vẽ các đường thẳng d₁ và d₂ trên cùng 1 mặt phẳng tọa độ . Tìm tọa độ giao điểm của 2 đường thẳng d₁ và d₂.

b) Tìm giá trị của m để đường thẳng d₁ cắt trục hoành tại điểm có hoành độ bằng –3

c) Chứng minh rằng đường thẳng d₁ luôn đi qua một điểm cố định với mọi giá trị của m.

Xem lời giải

Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

a) Với m = 2 thì ta có: d₁: y = 2x + 3; d₂: y = x + 1

Vẽ đường thằng đi qua 2 điểm A(0;3) và B\(\left( {\frac{{ - 3}}{2};0} \right)\) ta được d₁

Vẽ đường thẳng đi qua 2 điểm C(0;1) và D(–1; 0) ta được d₂

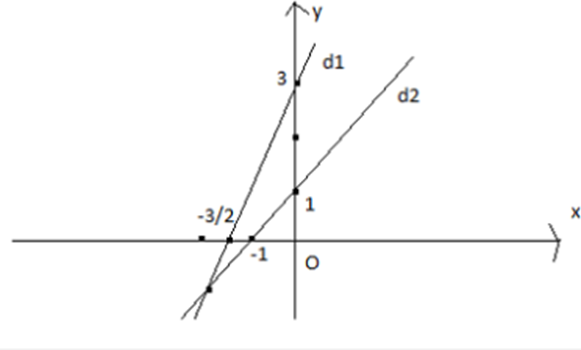
Cho đường thẳng d1: y = mx + 2m - 1 ( với m là tham số) và d2: y = x + 1 (ảnh 1)

Xét phương trình hoành độ giao điểm ta có:

2x + 3 = x + 1

⇔ x = – 2

Suy ra: y = –1

Vậy 2 đường thẳng cắt nhau tại E(–2; –1).

b) d₁ cắt trục hoành tại điểm có hoành độ bằng –3 tức là cắt tại điểm P(–3 ;0)

Khi đó ta có: 0 = –3m + 2m – 1

⇔ m = – 1

c) Gọi điểm cố định mà d₁ luôn đi qua là M(x₀; y₀)

Ta có: y₀ = mx₀ + 2m – 1 = m(x₀ + 2) – 1

⇔ m(x₀ + 2) = 1 + y₀

Để phương trình đúng với mọi m thì:

\(\left\{ \begin{array}{l}{x_0} + 2 = 0\\{y_0} + 1 = 0\end{array} \right.\) ⇔ \(\left\{ \begin{array}{l}{x_0} = - 2\\{y_0} = - 1\end{array} \right.\)

Vậy d₁ luôn đi qua điểm cố định là M(–2;–1).

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
Đăng ký ngay

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Có 4 cặp vợ chồng được xếp ngồi trên 1 chiếc ghế dài có 8 chỗ. Biết rằng mỗi người vợ chỉ ngồi cạnh chồng mình hoặc ngồi cạnh 1 người phụ nữ khác. Hỏi có bao nhiêu cách sắp xếp chỗ ngồi thỏa mãn?

Xem đáp án

Lời giải

Trường hợp 1: Xếp 4 người vợ ngồi cạnh nhau có 4! cách

+) Xếp 4 người chồng ngồi cạnh nhau VVVVCCCC hoặc CCCCVVVV có 2 cách

Vợ chỉ được ngồi cạnh chồng của mình nên, xếp 3 người chồng (không được gạch chân) Có 3! cách xếp

⇒ có 4!.2.3! cách

+) Xếp 3 người chồng ngồi cạnh nhau CVVVVCCC hoặc CCCVVVVC có 2 cách xếp

Xếp 2 người chồng (không được gạch chân) có 2 cách xếp

⇒ có 4!.2.2 cách

+) Xếp 2 người chồng ngồi cạnh nhau CCVVVVCC có 1 cách

Xếp 2 người chồng (không được gạch chân) có 2 cách xếp

⇒ có 4!.2

Vậy trường hợp 1 có 4!.2.3! + 4!.2.2 + 4!.2 = 432cách.

Trường hợp 2: Xếp 3 người vợ ngồi cạnh nhau

Xếp 4 người vợ vào 4 vị trí có 4! cách

+) 4 người chồng ngồi cạnh nhau: VCCCCVVV hoặc VVVCCCCV có 2 cách

Xếp 2 người chồng không được gạch chân có 2 cách xếp

⇒ có: 4!.2.2 cách

+) 3 người chồng ngồi cạnh nhau: VCCCVVVC hoặc CVVVCCCV có 2 cách

⇒ có: 4!.2 cách
+ 2 người chồng ngồi cạnh nhau: VCCVVVCC hoặc CCVVVCCVcó 2 cách xếp

⇒ có: 4!.2 cách

Vậy trường hợp này có 4!.2.2 + 4!.2 + 4!.2 = 192

Trường hợp 3: 2 người vợ ngồi cạnh nhau

Xếp 4 người vợ vào 4 vị trí có 4! cách

+) 4 người chồng ngồi cạnh nhau VVCCCCVV có 1 cách

Có 2 cách xếp 2 người chồng không có gạch chân

⇒ có: 4!.2

+) 3 người chồng ngồi cạnh nhau VVCCCVVC hoặc CVVCCCVV có 2 cách

⇒ có: 4!.2

+) 2 người chồng ngồi cạnh nhau CVVCCVVC hoặc VVCCVVCC hoặc CCVVCCVV hoặc VCCVVCCV có 4 cách xếp

⇒ có: 4!.4

Vậy trường hợp 3 có 4!.2 + 4!.2 + 4!.4 = 192 cách

Vậy có tất cả số cách là:

432 + 192 + 192 = 816 cách.

Câu 2

Cách bấm phím mode trên máy tính casio fx–580VNX.

Xem đáp án

Lời giải

Phím mode trong casio fx–580VN X đã được thay thế bằng phím Menu Setup.

Phím Menu Setup nằm ở trên cùng, bên trái nút ON.

Câu 3