Cho đường tròn (O) và điểm I không nằm trên đường tròn. Qua điểm I kẻ 2 dây cung AB và CD (A nằm giữa I và B, C nằm giữa I và D.
a) So sánh các cặp góc \(\widehat {ACI}\) và \(\widehat {ABD}\), \(\widehat {CAI}\) và \(\widehat {CDB\;}\).
b) Chứng minh các tam giác IAC và IDB đồng dạng.
c) Chứng minh IA.IB = IC. ID.
Cho đường tròn (O) và điểm I không nằm trên đường tròn. Qua điểm I kẻ 2 dây cung AB và CD (A nằm giữa I và B, C nằm giữa I và D.
a) So sánh các cặp góc \(\widehat {ACI}\) và \(\widehat {ABD}\), \(\widehat {CAI}\) và \(\widehat {CDB\;}\).
b) Chứng minh các tam giác IAC và IDB đồng dạng.
c) Chứng minh IA.IB = IC. ID.
Quảng cáo
Trả lời:
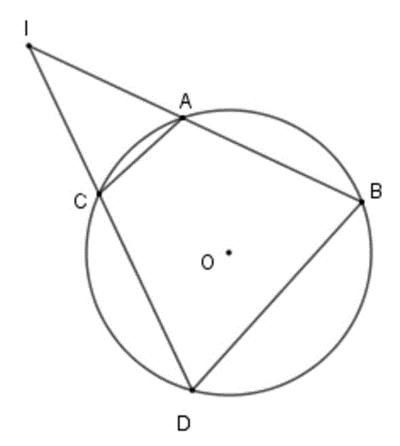
a) So sánh \(\widehat {ACI}\) và \(\widehat {ABD}\)
Ta có: \(\widehat {ACI} + \widehat {ACD} = 180^\circ \) (2 góc kề bù) (1)
Xét (O) có: \(\widehat {ABD}\) là góc nội tiếp chắn cung AD
\(\widehat {ACD}\) là góc nội tiếp chắn cung AD
Suy ra: \(\widehat {ABD} + \widehat {ABD} = \frac{1}{2}.360^\circ = 180^\circ \)(2)
Từ (1) và (2) suy ra: \(\widehat {ACI} = \widehat {ABD} = 180^\circ - \widehat {ACD}\)
* So sánh \(\widehat {CAI}\) và \(\widehat {CDB\;}\)
Ta có: \(\widehat {CAI} + \widehat {BAC} = 180^\circ \) (2 góc kề bù) (1)
Xét (O) có: \(\widehat {BAC}\) là góc nội tiếp chắn cung AD
\(\widehat {CDB}\) là góc nội tiếp chắn cung AD
Suy ra: \(\widehat {BAC} + \widehat {CDB} = \frac{1}{2}.360^\circ = 180^\circ \)(2)
Từ (1) và (2) suy ra: \(\widehat {CAI} = \widehat {CDB} = 180^\circ - \widehat {BAC}\)
b) Xét hai tam giác ΔIAC và ΔIDB có:
\(\widehat A\)chung
\(\widehat {IAC} = \widehat {IDB}\)(câu a)
Suy ra: ΔIAC ∽ ΔIDB (g.g).
c) Theo câu b có ΔIAC ∽ ΔIDB.
Suy ra: \(\frac{{IA}}{{ID}} = \frac{{IC}}{{IB}}\) hay IA.IB = IC.ID (đpcm).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Trường hợp 1: Xếp 4 người vợ ngồi cạnh nhau có 4! cách
+) Xếp 4 người chồng ngồi cạnh nhau VVVVCCCC hoặc CCCCVVVV có 2 cách
Vợ chỉ được ngồi cạnh chồng của mình nên, xếp 3 người chồng (không được gạch chân) Có 3! cách xếp
⇒ có 4!.2.3! cách
+) Xếp 3 người chồng ngồi cạnh nhau CVVVVCCC hoặc CCCVVVVC có 2 cách xếp
Xếp 2 người chồng (không được gạch chân) có 2 cách xếp
⇒ có 4!.2.2 cách
+) Xếp 2 người chồng ngồi cạnh nhau CCVVVVCC có 1 cách
Xếp 2 người chồng (không được gạch chân) có 2 cách xếp
⇒ có 4!.2
Vậy trường hợp 1 có 4!.2.3! + 4!.2.2 + 4!.2 = 432cách.
Trường hợp 2: Xếp 3 người vợ ngồi cạnh nhau
Xếp 4 người vợ vào 4 vị trí có 4! cách
+) 4 người chồng ngồi cạnh nhau: VCCCCVVV hoặc VVVCCCCV có 2 cách
Xếp 2 người chồng không được gạch chân có 2 cách xếp
⇒ có: 4!.2.2 cách
+) 3 người chồng ngồi cạnh nhau: VCCCVVVC hoặc CVVVCCCV có 2 cách
⇒ có: 4!.2 cách
+ 2 người chồng ngồi cạnh nhau: VCCVVVCC hoặc CCVVVCCVcó 2 cách xếp
⇒ có: 4!.2 cách
Vậy trường hợp này có 4!.2.2 + 4!.2 + 4!.2 = 192
Trường hợp 3: 2 người vợ ngồi cạnh nhau
Xếp 4 người vợ vào 4 vị trí có 4! cách
+) 4 người chồng ngồi cạnh nhau VVCCCCVV có 1 cách
Có 2 cách xếp 2 người chồng không có gạch chân
⇒ có: 4!.2
+) 3 người chồng ngồi cạnh nhau VVCCCVVC hoặc CVVCCCVV có 2 cách
⇒ có: 4!.2
+) 2 người chồng ngồi cạnh nhau CVVCCVVC hoặc VVCCVVCC hoặc CCVVCCVV hoặc VCCVVCCV có 4 cách xếp
⇒ có: 4!.4
Vậy trường hợp 3 có 4!.2 + 4!.2 + 4!.4 = 192 cách
Vậy có tất cả số cách là:
432 + 192 + 192 = 816 cách.
Lời giải
Phím mode trong casio fx–580VN X đã được thay thế bằng phím Menu Setup.
Phím Menu Setup nằm ở trên cùng, bên trái nút ON.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.