Câu hỏi:
11/07/2024 3,670
Cho ΔABCΔABC vuông tại A (AB < AC) và đường cao AH. Từ H kẻ HE ⊥ AB, HF ⊥ AC (E ∈ AB; F ∈ AC).
a) Chứng minh tứ giác AEHF là hình chữ nhật.
b) Gọi D là điểm đối xứng của A qua F. Chứng minh DHEF là hình bình hành.
c) Gọi I là giao điểm của EF và AH; M là trung điểm của BC. Qua A kẻ tia Ax vuông góc với đường thẳng MI cắt tia CB tại K. Chứng minh 4 điểm K, E, I, F thẳng hàng.
Cho ΔABCΔABC vuông tại A (AB < AC) và đường cao AH. Từ H kẻ HE ⊥ AB, HF ⊥ AC (E ∈ AB; F ∈ AC).
a) Chứng minh tứ giác AEHF là hình chữ nhật.
b) Gọi D là điểm đối xứng của A qua F. Chứng minh DHEF là hình bình hành.
c) Gọi I là giao điểm của EF và AH; M là trung điểm của BC. Qua A kẻ tia Ax vuông góc với đường thẳng MI cắt tia CB tại K. Chứng minh 4 điểm K, E, I, F thẳng hàng.
Quảng cáo
Trả lời:
Giải bởi Vietjack
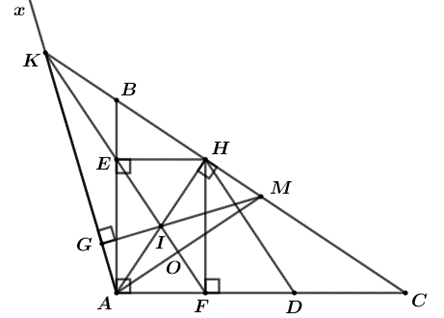
a) Chứng minh tứ giác AEHF là hình chữ nhật.
ΔABC vuông tại A ⇒ \(\widehat {BAC}\)= 90°
Vì HE⊥AB, HF⊥AC nên \(\widehat {HEA}\)= 90°, \(\widehat {HFA}\)= 90°
Xét tứ giác AEHF ta có:
\(\widehat {HEA} = \widehat {HFA} = \widehat {EAF}\)= 90°
Suy ra, tứ giác AEHF là hình chữ nhật (dấu hiệu nhận biết).
b) Gọi D là điểm đối xứng của A qua F.
Vì AEHF là hình chữ nhật suy ra EH // AF và EH = AF (tính chất của hình chữ nhật)
Vì D là tâm đối xứng của A qua F nên F là trung điểm của AD. Suy ra, AF = FD.
Do đó, EH // FD và EH = FD.
Suy ra, DHEF là hình bình hành (dấu hiệu nhận biết)
c)
+) Vì I là giao điểm của EF và AH nên ba điểm E, I, F thẳng hàng.
+) Gọi O là giao điểm của EF và AM.
Vì AM là đường trung tuyến của ΔABCΔABC nên AM = MC suy ra ΔAMC cân tại M. Do đó, \(\widehat {MAC} = \widehat {MCA}\)
Vì EHFA là hình chữ nhật, có I là giao điểm hai đường chéo nên ta có \(\widehat {IAF} = \widehat {IFA}\)
Xét ΔAHC ta có: \(\widehat {HAC} + \widehat {HCA} = 90^\circ \) hay \(\widehat {IAF} + \widehat {MCA} = 90^\circ \)
⇒ \(\widehat {IAF} + \widehat {MAC} = 90^\circ \) hay \(\widehat {OAF} + \widehat {OFA} = 90^\circ \)
Xét ΔOAF có: \(\widehat {OAF} + \widehat {OFA} = 90^\circ \)⇒ \(\widehat {AOF} = 90^\circ \)
⇒ EF vuông góc với AM tại O hay IF vuông góc với AM tại O.
+) Xét ΔKAM ta có:
GM ⊥ KA tại G
AH ⊥ KM tại H
Mà I là giao điểm của AH và GM nên I là trực tâm của ΔKAM.
⇒ KI ⊥ AM mà IF ⊥ AM
⇒ K, I, F thẳng hàng.
Ta có:
Ba điểm E, I, F thẳng hàng.
Ba điểm K, I, F thẳng hàng.
⇒ Bốn điểm I, K, E, F thẳng hàng.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Trường hợp 1: Xếp 4 người vợ ngồi cạnh nhau có 4! cách
+) Xếp 4 người chồng ngồi cạnh nhau VVVVCCCC hoặc CCCCVVVV có 2 cách
Vợ chỉ được ngồi cạnh chồng của mình nên, xếp 3 người chồng (không được gạch chân) Có 3! cách xếp
⇒ có 4!.2.3! cách
+) Xếp 3 người chồng ngồi cạnh nhau CVVVVCCC hoặc CCCVVVVC có 2 cách xếp
Xếp 2 người chồng (không được gạch chân) có 2 cách xếp
⇒ có 4!.2.2 cách
+) Xếp 2 người chồng ngồi cạnh nhau CCVVVVCC có 1 cách
Xếp 2 người chồng (không được gạch chân) có 2 cách xếp
⇒ có 4!.2
Vậy trường hợp 1 có 4!.2.3! + 4!.2.2 + 4!.2 = 432cách.
Trường hợp 2: Xếp 3 người vợ ngồi cạnh nhau
Xếp 4 người vợ vào 4 vị trí có 4! cách
+) 4 người chồng ngồi cạnh nhau: VCCCCVVV hoặc VVVCCCCV có 2 cách
Xếp 2 người chồng không được gạch chân có 2 cách xếp
⇒ có: 4!.2.2 cách
+) 3 người chồng ngồi cạnh nhau: VCCCVVVC hoặc CVVVCCCV có 2 cách
⇒ có: 4!.2 cách
+ 2 người chồng ngồi cạnh nhau: VCCVVVCC hoặc CCVVVCCVcó 2 cách xếp
⇒ có: 4!.2 cách
Vậy trường hợp này có 4!.2.2 + 4!.2 + 4!.2 = 192
Trường hợp 3: 2 người vợ ngồi cạnh nhau
Xếp 4 người vợ vào 4 vị trí có 4! cách
+) 4 người chồng ngồi cạnh nhau VVCCCCVV có 1 cách
Có 2 cách xếp 2 người chồng không có gạch chân
⇒ có: 4!.2
+) 3 người chồng ngồi cạnh nhau VVCCCVVC hoặc CVVCCCVV có 2 cách
⇒ có: 4!.2
+) 2 người chồng ngồi cạnh nhau CVVCCVVC hoặc VVCCVVCC hoặc CCVVCCVV hoặc VCCVVCCV có 4 cách xếp
⇒ có: 4!.4
Vậy trường hợp 3 có 4!.2 + 4!.2 + 4!.4 = 192 cách
Vậy có tất cả số cách là:
432 + 192 + 192 = 816 cách.
Lời giải
Gọi a là chiều dài đúng của cây cầu
Suy ra: a = 152m ± 0,2m
⇒ 152 – 0,2 ≤ a ≤ 152 + 0,2
⇒ 151,8 ≤ a ≤ 152,2
Vậy chiều dài đúng của cây cầu là một số nằm trong khoảng 151,8m đến 152,2m
Sai số tương đối = 0,2 : 152 . 100% ≈ 0,13%.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo