Câu hỏi:

19/08/2025 7,758

Từ một điểm A nằm ngoài đường tròn (O; R) vẽ hai tiếp tuyến AB, AC với đường tròn (B, C là tiếp điểm). Trên cung nhỏ BC lấy một điểm M bất kỳ, vẽ MI vuông góc với AB, MK vuông góc với AC (I thuộc AB, K thuộc AC).

a) Chứng minh AIMK, ABOC là các tứ giác nội tiếp;

b) Vẽ MP vuông góc với BC (P thuộc BC). Chứng minh ;

c) Chứng minh MI.MK = MP²;

d) Xác định vị trí của điểm M trên cung nhỏ BC để tích MI.MK.MP đạt giá trị lớn nhất.

Xem lời giải

Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

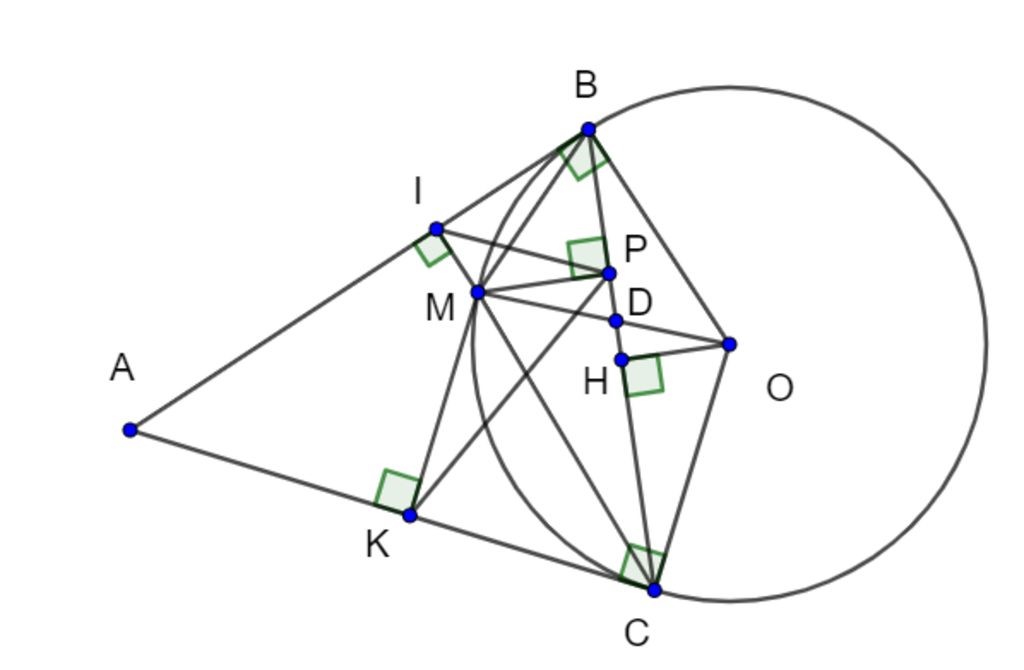
Media VietJack

a) Xét tứ giác AIMK có:

$\hat{A I M}$ = 90° (MI ⊥ AB); $\hat{A K M}$ = 90° (MK ⊥ AC)

⇒ $\hat{A I M} + \hat{A K M}$ = 90° + 90° = 180°

Mà 2 góc ở vị trí đối nhau

⇒ Tứ giác AIMK nội tiếp

Xét (O) có AB, AC là hai tiếp tuyến cắt nhau tại A

⇒ OB ⊥ AB; OC ⊥ AC ⇒ $\hat{A B O} = \hat{A C O}$ = 90°

Xét tứ giác ABOC có:

$\hat{A B O} + \hat{A C O}$ = 90° + 90° = 180°

Mà 2 góc ở vị trí đối nhau

⇒ Tứ giác ABOC nội tiếp

b) Xét tứ giác MPCK có:

$\hat{M P C}$ = 90° (MP ⊥ BC); $\hat{M K C}$ = 90° (MK ⊥ AC)

⇒ $\hat{M P C} + \hat{M K C}$ = 90° + 90° = 180°

Mà 2 góc ở vị trí đối nhau

⇒ Tứ giác MPCK nội tiếp

⇒ $\hat{M P K} = \hat{M C K}$ (cùng nhìn cạnh MK)

Xét (O) có: $\hat{M C K}$ là góc tạo bởi tiếp tuyến và dây cung MC

$\hat{M B C}$ là góc nội tiếp chắn cung MC

⇒ $\hat{M C K} = \hat{M B C}$

Mà $\hat{M P K} = \hat{M C K}$ ⇒ $\hat{M P K} = \hat{M B C}$

c) Xét tứ giác MIBP có:

$\hat{M I B}$ = 90° (MI ⊥ AB) ; $\hat{M P B}$ = 90°(MP⊥BC)

⇒ $\hat{M I B} + \hat{M P B}$ = 90° + 90° = 180°

mà 2 góc ở vị trí đối nhau

⇒Ttứ giác MIBP nội tiếp

⇒ $\hat{I B M} = \hat{I P M}$ (cùng nhìn cạnh MI)

$\hat{M I P} = \hat{M B P}$ (cùng nhìn cạnh MP) hay $\hat{M B C} = \hat{M I P}$

mà $\hat{M P K} = \hat{M B C}$ ⇒ $\hat{M P K} = \hat{M I P}$

Xét (O) có: $\hat{I B M}$ là góc tạo bởi tiếp tuyến và dây cung BM

$\hat{M C B}$ là góc nội tiếp chắn cung BM

⇒ $\hat{I B M} = \hat{M C B}$

mà $\hat{I B M} = \hat{I P M}$ ⇒ $\hat{M C B} = \hat{I P M}$ hay $\hat{M C P} = \hat{I P M}$

Tứ giác MPCK nội tiếp ⇒ $\hat{M C P} = \hat{M K P}$

⇒ $\hat{I P M} = \hat{M K P}$

Xét ΔMIP và ΔMPK có:

$\hat{I P M} = \hat{M K P}$

$\hat{M I P} = \hat{M P K}$

⇒ ΔMIP ~ ΔMPK (g.g)

⇒ MI.MP = MP.MK ⇒ MI.MK = MP²

d) Vì MI.MK = MP² nên MI.MK.MP = MP³

Tích MI.MK.MP đạt giá trị lớn nhất khi MP lớn nhất

Gọi H là hình chiếu của O trên BC

⇒ OH cố định (Vì O cố định; BC cố định)

Gọi D là giao điểm của MO và BC

Ta có: MP ≤ MD; OH ≤ OD

MP + OH ≤ MD + OD = MO ⇒ MP + OH ≤ R

⇒MP ≤ R−OH ⇒ MP³ ≤ (R − OH)³

Dấu "=" xảy ra khi MP = R − OH

⇒ O, H, Mthẳng hàng

⇒ M nằm chính giữa cung nhỏ BC

Vậy tích MI.MK.MP đạt giá trị lớn nhất khi M nằm chính giữa cung nhỏ BC.

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
Đăng ký ngay

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho sin α = $\frac{1}{3},$ với 90° < α < 180°. Tính cos α.

Xem đáp án

Lời giải

sin²α = ${(\frac{1}{3})}^{2} = \frac{1}{9}$

Ta có: sin²α + cos²α = 1

Suy ra: cos²α = 1 – sin²α = $1 - \frac{1}{9} = \frac{8}{9}$

cos α = $\pm \sqrt{\frac{8}{9}} = \pm \frac{2 \sqrt{2}}{3}$

Vì 90° < α < 180° nên cos α = $- \frac{2 \sqrt{2}}{3}$

Câu 2

Cho đường tròn (O) và một điểm A nằm ngoài đường tròn (O). Từ A vẽ hai tiếp tuyến AB, AC của đường tròn (O) (B và C là hai tiếp điểm). Gọi H là giao điểm của OA và BC.

a) Chứng minh OA vuông góc với BC tại H.

b) Từ B vẽ đường kính BD của (O), đường thẳng AD cắt đường tròn (O) tại E (khác D), Chứng minh: AE.AD = AH.AO.

Xem đáp án

Lời giải

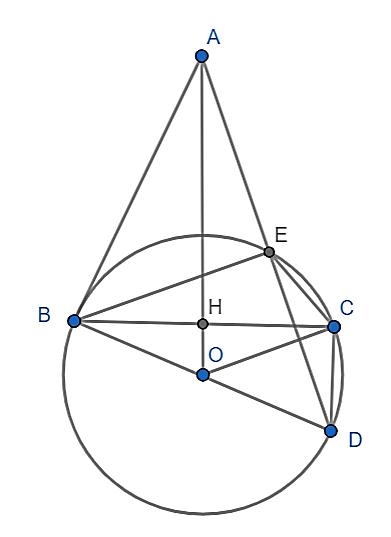
Media VietJack

a) Vì AB, AC là tiếp tuyến của (O)

⇒ AB = AC mà OB = OC⇒ AO là đường trung trực của BC

⇒ OA ⊥ BC

b) Xét ΔACE và ΔADC có:

$\hat{A C E} = \hat{A D C}$ (góc tạo bởi tiếp tuyến, dây cung và góc nội tiếp cùng chắn cung EC)

$\hat{E A C} = \hat{D A C}$

⇒ ΔACE ∼ ΔADC (g.g)

⇒ $\frac{A C}{A D} = \frac{A E}{A C}$

⇒ AE.AD = AC² = AH.AO (ΔACO vuông tại C có CH là đường cao)

Câu 3