Câu hỏi:
13/07/2024 2,382
Cho hình chóp S.ABCD có đáy ABCD là hình thang với AB // CD và AB = 2DC. Gọi O là giao điểm của AC và BD, G là trọng tâm tam giác SBC, H là giao điểm của DG và (SAC). Tính tỉ số \[\frac{{GH}}{{GD}}\].
Cho hình chóp S.ABCD có đáy ABCD là hình thang với AB // CD và AB = 2DC. Gọi O là giao điểm của AC và BD, G là trọng tâm tam giác SBC, H là giao điểm của DG và (SAC). Tính tỉ số \[\frac{{GH}}{{GD}}\].
Quảng cáo
Trả lời:
Giải bởi Vietjack
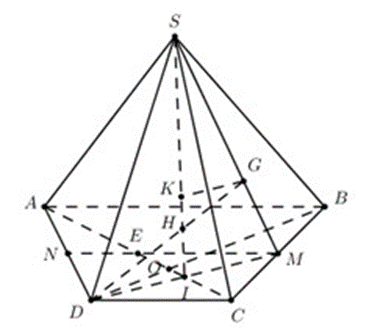
Gọi M là trung điểm của BC, I = AC ∩ DM .
Trong (SDM) gọi H = DG ∩ SI ta có:
• I ∈ AC ⇒ I ∈ (SAC) ⇒ SI ⊂ SAC
• H ∈ SI ⇒ H ∈ (SAC) ⇒ H = DG ∩ (SAC).
Gọi N là trung điểm của AD, E = AC ∩ MN
Nên MN là đường trung bình của hình thang ABCD
\[ \Rightarrow MN = \frac{{AB + CD}}{2} = \frac{{2CD + CD}}{2} = \frac{{3CD}}{2}\]
Áp dụng định lí Ta-lét, ta có:
• \[\frac{{NE}}{{CD}} = \frac{{AN}}{{AD}} = \frac{1}{2} \Rightarrow NE = \frac{1}{2}CD \Rightarrow ME = \frac{3}{2}CD - \frac{1}{2}CD = CD\]
• \[\frac{{IM}}{{ID}} = \frac{{CD}}{{MN}} = \frac{{ME}}{{CD}} = 1 \Rightarrow IM = ID\]
Kẻ GK // DM, áp dụng định lí Vi-ét ta có:
\[\frac{{GH}}{{DH}} = \frac{{KG}}{{ID}} = \frac{{KG}}{{IM}} = \frac{{KG}}{{IM}} = \frac{{SG}}{{SM}} = \frac{2}{3}\]
\[ \Rightarrow \frac{{GH}}{{GH + DH}} = \frac{2}{{2 + 3}} = \frac{2}{5} \Rightarrow \frac{{GH}}{{GD}} = \frac{2}{5}\].
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
(sin2 x)’ = 2sin x.(sin x)’ = 2sin x cos x = sin 2x.
Vậy đạo hàm của hàm số sin2 x là sin 2x.
Lời giải
Ta có: cosx ∈ [−1; 1]
Để phương trình có nghiệm thì:
− 1 ≤ m − 1 ≤ 1 suy ra 0 ≤ m ≤ 2
Vậy m ∈ [0; 2].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
20 câu Trắc nghiệm Phương trình đường thẳng trong không gian có đáp án (Nhận biết)