Câu hỏi:
15/08/2023 921
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh \[2\sqrt 2 \], cạnh bên SA vuông góc với mặt đáy. Mặt phẳng (α) qua A và vuông góc với SC cắt các cạn SB, SC, SD lần lượt tại các điểm M, N, P. Tính thể tích V của khối cầu ngoại tiếp tứ diện CMNP.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh \[2\sqrt 2 \], cạnh bên SA vuông góc với mặt đáy. Mặt phẳng (α) qua A và vuông góc với SC cắt các cạn SB, SC, SD lần lượt tại các điểm M, N, P. Tính thể tích V của khối cầu ngoại tiếp tứ diện CMNP.
Quảng cáo
Trả lời:
Giải bởi Vietjack
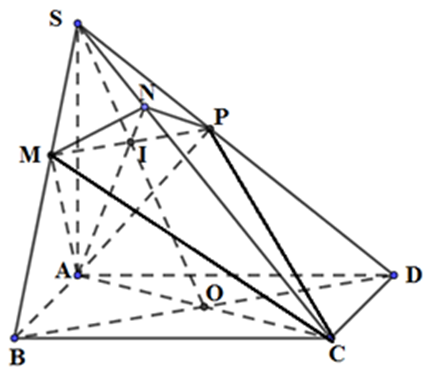
Gọi O là tâm của hình vuông ABCD ⇒O là trung điểm của AC
Ta có: CD ^ AD; CD ^ SA
Þ CD ^ (SAD)
Þ CD ^ AP
Lại có: SC ^ AP (do SC ⊥ (α)); CD ⊥ AP
⇒ AP ⊥ (SCD) ⇒ AP ⊥ CP ⇒ ΔAPC vuông tại P
⇒ OA = OC = OP
Tương tự, ta có: ΔAMC vuông tại M
⇒ OA = OC = OM
Lại có: SC ⊥ AN (do SC ⊥ (α))
⇒ΔANC vuông tại N ⇒OA = OC = ON
⇒ OA = OC = OP = OM = ON
Þ O là tâm mặt cầu ngoại tiếp tứ diện CMNP
Bán kính khối cầu là:
\[R = OA = \frac{{AB}}{{\sqrt 2 }} = 2\]
Thể tích khối cầu ngoại tiếp tứ diện CMNP là:
\[V = \frac{{4\pi }}{3} \cdot {2^3} = \frac{{32\pi }}{3}\]
Vậy thể tích khối cầu ngoại tiếp tứ diện CMNP là \[\frac{{32\pi }}{3}\].
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
(sin2 x)’ = 2sin x.(sin x)’ = 2sin x cos x = sin 2x.
Vậy đạo hàm của hàm số sin2 x là sin 2x.
Lời giải
Ta có: cosx ∈ [−1; 1]
Để phương trình có nghiệm thì:
− 1 ≤ m − 1 ≤ 1 suy ra 0 ≤ m ≤ 2
Vậy m ∈ [0; 2].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
20 câu Trắc nghiệm Phương trình đường thẳng trong không gian có đáp án (Nhận biết)