Câu hỏi:
13/07/2024 1,126
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng 2a. Gọi M là trung điểm của SD. Giá trị tang của góc giữa đường thẳng BM và mặt phẳng (ABCD) bằng?
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng 2a. Gọi M là trung điểm của SD. Giá trị tang của góc giữa đường thẳng BM và mặt phẳng (ABCD) bằng?
Quảng cáo
Trả lời:
Giải bởi Vietjack
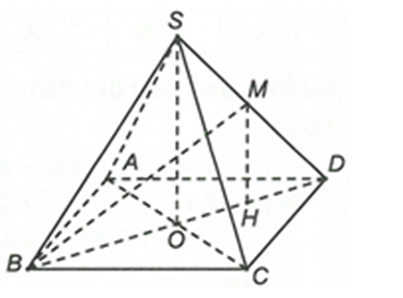
Gọi {O} = AC ∩ BD nên SO ⊥ (ABCD).
Gọi H là trung điểm của OD.
Xét ∆SOD có MH là đường trung bình nên MH // SO.
Suy ra MH ⊥ (ABCD).
Hình chiếu của đường thẳng BM trên mặt phẳng (ABCD) là BH.
Suy ra \[\widehat {\left( {BM,\left( {ABCD} \right)} \right)} = \widehat {\left( {BM,BH} \right)} = \widehat {MBH}\] là góc nhọn
Xét tam giác vuông ABD có:
\[BD = \sqrt {A{B^2} + A{D^2}} = \sqrt {{{\left( {2a} \right)}^2} + {{\left( {2a} \right)}^2}} = 2\sqrt 2 a.\]
\[ \Rightarrow BH = \frac{3}{4}BD = \frac{{3\sqrt 2 a}}{2}\]và \[OD = \frac{1}{2}BD = \sqrt 2 a.\]
Xét tam giác vuông SOD có:
\[SO = \sqrt {S{D^2} - O{D^2}} = \sqrt {{{\left( {2a} \right)}^2} - {{\left( {\sqrt 2 a} \right)}^2}} = \sqrt 2 a.\]
Suy ra \[MH = \frac{1}{2}SO = \frac{{\sqrt 2 a}}{2}.\]
Ta có \[\tan \widehat {MBH} = \frac{{MH}}{{BH}} = \frac{{\frac{{a\sqrt 2 }}{2}}}{{\frac{{a\sqrt 2 a}}{2}}} = \frac{1}{3}\].
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
(sin2 x)’ = 2sin x.(sin x)’ = 2sin x cos x = sin 2x.
Vậy đạo hàm của hàm số sin2 x là sin 2x.
Lời giải
Ta có: cosx ∈ [−1; 1]
Để phương trình có nghiệm thì:
− 1 ≤ m − 1 ≤ 1 suy ra 0 ≤ m ≤ 2
Vậy m ∈ [0; 2].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
20 câu Trắc nghiệm Phương trình đường thẳng trong không gian có đáp án (Nhận biết)