Câu hỏi:
13/07/2024 971
Cho hình chữ nhật ABCD (AB > BC). Từ B kẻ BH vuông góc với AC tại H. Lấy E sao cho H là trung điểm BE, lấy Q đối xứng với C qua H. QE cắt DC tại M. Gọi N là hình chiếu của E trên AD, MN cắt DE tại O. Chứng minh tam giác OEM là tam giác cân.
Cho hình chữ nhật ABCD (AB > BC). Từ B kẻ BH vuông góc với AC tại H. Lấy E sao cho H là trung điểm BE, lấy Q đối xứng với C qua H. QE cắt DC tại M. Gọi N là hình chiếu của E trên AD, MN cắt DE tại O. Chứng minh tam giác OEM là tam giác cân.
Quảng cáo
Trả lời:
Giải bởi Vietjack
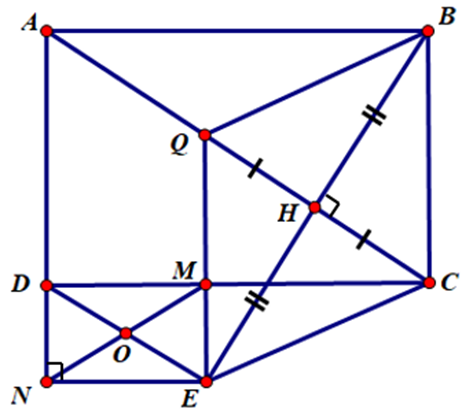
Ta có: NE ^ AD; DM ^ AD
Þ DM // NE
Xét tứ giác BCEQ có: BE ^ QC = {H}
H là trung điểm của QC
H là trung điểm của BE
Do đó BCEQ là hình thoi, suy ra BC // QE.
Mà BC // AD nên QE // AD
Xét tứ giác DMEN có: DM // NE; QE // DN
Suya ra tứ giác DMEN là hình bình hành
Mà \[\widehat {NDM} = 90^\circ \] nên tứ giác DMEN là hình chữ nhật
Do đó OM = OE
Vậy tam giác OME cân tại O.
Sách thầy cô Vietjack biên soạn
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Một trường có 50 học sinh giỏi trong đó có 4 cặp anh em sinh đôi. Cần chọn ra 3 học sinh trong số 50 học sinh để tham dự trại hè. Tính xác suất trong 3 em ấy không có cặp anh em sinh đôi?
Một trường có 50 học sinh giỏi trong đó có 4 cặp anh em sinh đôi. Cần chọn ra 3 học sinh trong số 50 học sinh để tham dự trại hè. Tính xác suất trong 3 em ấy không có cặp anh em sinh đôi?
Xem đáp án »
13/07/2024
6,381
Câu 4:
Cho tập A = {0; 1; 2; 3; 4; 5; 6}. Gọi X là tập các số tự nhiên có 5 chữ số khác nhau được lập từ A. Chọn một số từ X, tính xác suất sao cho số được chọn có đúng 3 chữ số chẵn.
Cho tập A = {0; 1; 2; 3; 4; 5; 6}. Gọi X là tập các số tự nhiên có 5 chữ số khác nhau được lập từ A. Chọn một số từ X, tính xác suất sao cho số được chọn có đúng 3 chữ số chẵn.
Xem đáp án »
13/07/2024
4,275
Câu 5:
Cho hàm số f(x) thỏa mãn \[f\left( 2 \right) = - \frac{2}{9}\]và f ′(x) = 2x[f(x)]2 với mọi \[x \in \mathbb{R}\]. Tính giá trị của f(1).
Cho hàm số f(x) thỏa mãn \[f\left( 2 \right) = - \frac{2}{9}\]và f ′(x) = 2x[f(x)]2 với mọi \[x \in \mathbb{R}\]. Tính giá trị của f(1).
Xem đáp án »
13/07/2024
3,714
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
80 câu Bài tập Hình học Khối đa diện có lời giải chi tiết (P1)
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)
-
148 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu từ đề thi Đại học có lời giải (P1)
-
62 câu Trắc nghiệm Khái niệm về khối đa diện (nhận biết)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận