Câu hỏi:
12/07/2024 2,821
Cho hình chóp S.ABCD, có đáy ABCD là hình chữ nhật với AB = a, \(AD = a\sqrt 2 \), SA = a và SA vuông góc với mặt phẳng (ABCD). Gọi M, N lần lượt là trung điểm của AD, SC. Giả sử I là giao điểm của BM và AC. Tính thể tích tứ diện ANIB.
Cho hình chóp S.ABCD, có đáy ABCD là hình chữ nhật với AB = a, \(AD = a\sqrt 2 \), SA = a và SA vuông góc với mặt phẳng (ABCD). Gọi M, N lần lượt là trung điểm của AD, SC. Giả sử I là giao điểm của BM và AC. Tính thể tích tứ diện ANIB.
Quảng cáo
Trả lời:
Giải bởi Vietjack
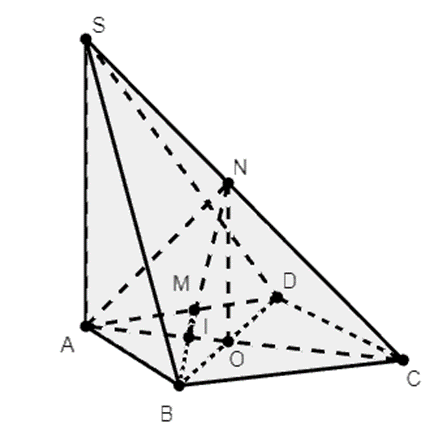
Gọi O là tâm của đáy ABCD.
Trong tam giác SAC, ta có NO là đường trung bình nên NO // SA.
Tức là NO ⊥ (ABCD) và \(NO = \frac{a}{2}\).
Ta có \({V_{ANIB}} = {V_{NAIB}} = \frac{1}{3}.{S_{AIB}}.NO = \frac{3}{6}.{S_{AIB}}(1)\)
Ta tính diện tích tam giác AIB:
Xét hình chữ nhật ABCD. Do MA = MD
\( \Rightarrow MA = \frac{1}{2}BD \Rightarrow AI = \frac{1}{2}IC\)
\( \Rightarrow AI = \frac{1}{3}AC \Rightarrow A{I^2} = \frac{{A{C^2}}}{9} = \frac{{2{a^2} + {a^2}}}{9} = \frac{{{a^2}}}{3}\)
Lại có \(BI = \frac{2}{3}BM \Rightarrow B{I^2} = \frac{4}{9}B{M^2} = \frac{4}{9}\left( {{a^2} + \frac{{{a^2}}}{2}} \right) = \frac{{2{a^2}}}{3}\)
Do đó AI2 + BI2 = a2 = AB2, nên AIB là tam giác vuông đỉnh I.
Vậy \({S_{AIB}} = \frac{1}{2}.IA.IB = \frac{1}{2}.\frac{{a\sqrt 3 }}{3}.\frac{{a\sqrt 6 }}{3} = \frac{{{a^2}\sqrt 2 }}{6}(2)\)
Thay (2) vào (1) ta có: \({V_{ANIB}} = \frac{{{a^3}\sqrt 2 }}{{36}}(dvtt)\)
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: D
Ta có: G là trọng tâm tam giác ABC nên:
\(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \)
\( \Rightarrow \overrightarrow {SA} - \overrightarrow {SG} + \overrightarrow {SB} - \overrightarrow {SG} + \overrightarrow {SC} - \overrightarrow {SG} = \overrightarrow 0 \)
\( \Leftrightarrow \overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} - 3\overrightarrow {SG} = \overrightarrow 0 \)
\( \Leftrightarrow \overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} = 3\overrightarrow {SG} \)
Vậy \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} = 3\overrightarrow {SG} \).
Lời giải
Đáp án đúng là: D
Dựa vào đồ thị ta có a > 0, đồ thị cắt Oy tại 1 điểm có tung độ dương nên d > 0, đồ thị có 2 cực trị trái dấu nên:
x1.x2 < 0 \( \Rightarrow \frac{c}{a} < 0\) ⇒ c < 0
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
140 câu Bài tập Hàm số mũ và Logarit cơ bản, nâng cao cực hay có lời giải chi tiết (P1)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận