Câu hỏi:
17/08/2023 229
Cho tam giác đều ABC nội tiếp đường tròn tâm I đường kính AA’, M là trung điểm của BC. Khi quay tam giác ABM cùng với nửa hình tròn đường kính AA’ xung quanh đường thẳng AM (như hình vẽ minh họa), ta được khối nón và khối cầu có thể tích lần lượt là V1 và V2. Tỉ số \(\frac{{{V_1}}}{{{V_2}}}\) bằng
Cho tam giác đều ABC nội tiếp đường tròn tâm I đường kính AA’, M là trung điểm của BC. Khi quay tam giác ABM cùng với nửa hình tròn đường kính AA’ xung quanh đường thẳng AM (như hình vẽ minh họa), ta được khối nón và khối cầu có thể tích lần lượt là V1 và V2. Tỉ số \(\frac{{{V_1}}}{{{V_2}}}\) bằng
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: D
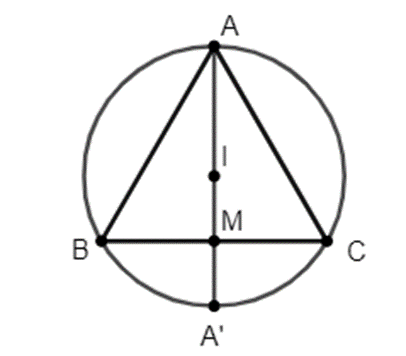
Giả sử tam giác ABC đều cạnh 1, khi đó ta có \(AM = \frac{{\sqrt 3 }}{2}\)
\( \Rightarrow AI = \frac{2}{3}.\frac{{\sqrt 3 }}{2} = \frac{{\sqrt 3 }}{3} = R\)
\( \Rightarrow {V_2} = \frac{4}{3}\pi .{R^3} = \frac{4}{3}\pi {\left( {\frac{{\sqrt 3 }}{3}} \right)^3} = \frac{{4\sqrt 3 }}{{27}}\)
\({V_1} = \frac{1}{3}\pi .B{M^2}.AM = \frac{1}{3}\pi .{\left( {\frac{1}{2}} \right)^2}.\frac{{\sqrt 3 }}{2} = \frac{{\sqrt 3 }}{{24}}\)
Vậy \(\frac{{{V_1}}}{{{V_2}}} = \frac{{\frac{{\sqrt 3 }}{{24}}}}{{\frac{{4\sqrt 3 }}{{27}}}} = \frac{9}{{32}}\)
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: D
Ta có: G là trọng tâm tam giác ABC nên:
\(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \)
\( \Rightarrow \overrightarrow {SA} - \overrightarrow {SG} + \overrightarrow {SB} - \overrightarrow {SG} + \overrightarrow {SC} - \overrightarrow {SG} = \overrightarrow 0 \)
\( \Leftrightarrow \overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} - 3\overrightarrow {SG} = \overrightarrow 0 \)
\( \Leftrightarrow \overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} = 3\overrightarrow {SG} \)
Vậy \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} = 3\overrightarrow {SG} \).
Lời giải
Đáp án đúng là: D
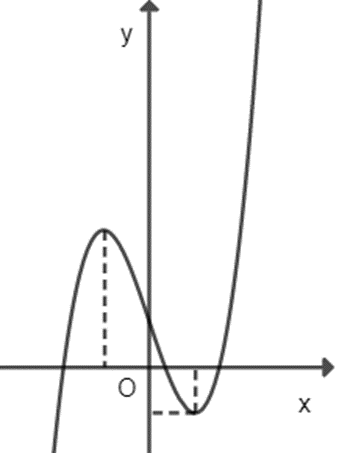
Dựa vào đồ thị ta có a > 0, đồ thị cắt Oy tại 1 điểm có tung độ dương nên d > 0, đồ thị có 2 cực trị trái dấu nên:
x1.x2 < 0 \( \Rightarrow \frac{c}{a} < 0\) ⇒ c < 0
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
140 câu Bài tập Hàm số mũ và Logarit cơ bản, nâng cao cực hay có lời giải chi tiết (P1)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận