Câu hỏi:

17/08/2023 259

Hai bạn Bình và Lan cùng dự thi trong kì thi THPT Quốc gia 2018 và ở hai phòng thi khác nhau. Mỗi phòng thi có 24 thí sinh, mỗi môn thi có 24 mã đề khác nhau. Đề thi được sắp xếp và phát cho thí sinh một cách ngẫu nhiên. Xác suất để hai môn thi Toán và Tiếng Anh, Bình và Lan có chung một mã đề thi bằng nhau là

A. \(\frac{{32}}{{135}}\).

B. \(\frac{{46}}{{2209}}\);

C. \(\frac{{23}}{{288}}\);

D. \(\frac{{23}}{{576}}\).

Xem lời giải

Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Đáp án đúng là: C

Hai bạn Bình và Lan có cùng 1 mã đề, cùng 1 môn thi (Toán hoặc Tiếng Anh) có 21 cách.

Môn còn lại khác nhau nên có 24.23 cách chọn,

Do đó có 2.24.24.23 = 26 496 cách để Bình và Lan có chung mã đề.

Vậy xác suất cần tìm là: \(P = \frac{{26\,\,496}}{{{{24}^2}\,.\,{{24}^2}}} = \frac{{23}}{{288}}\).

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hình chóp S.ABC, gọi G là trọng tâm tam giác ABC. Tìm mệnh đề đúng trong các mệnh đề sau:

A. \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} = 4\overrightarrow {SG} \);

B. \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} = \overrightarrow {SG} \);

C. \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} = 2\overrightarrow {SG} \);

D. \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} = 3\overrightarrow {SG} \).

Lời giải

Đáp án đúng là: D

Ta có: G là trọng tâm tam giác ABC nên:

\(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \)

\( \Rightarrow \overrightarrow {SA} - \overrightarrow {SG} + \overrightarrow {SB} - \overrightarrow {SG} + \overrightarrow {SC} - \overrightarrow {SG} = \overrightarrow 0 \)

\( \Leftrightarrow \overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} - 3\overrightarrow {SG} = \overrightarrow 0 \)

\( \Leftrightarrow \overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} = 3\overrightarrow {SG} \)

Vậy \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} = 3\overrightarrow {SG} \).

Câu 2

Cho hàm số y = ax³ + bx² + cx + d (a ≠ 0) có đồ thị nhứ hình vẽ dưới đây. Chọn khẳng định đúng về dấu của a, b, c, d.

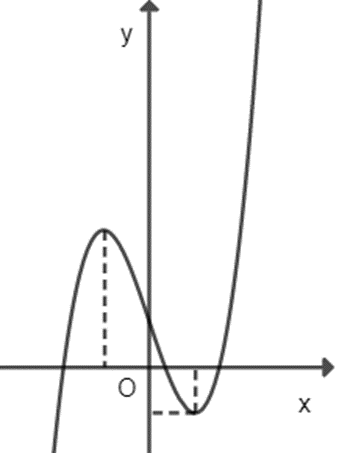
A. a > 0, b > 0, C > 0, d > 0;

B. a > 0, c > 0 > b, d < 0;

C. a > 0, b > 0, c > 0, d > 0;

D. a > 0, b < 0, c < 0, d > 0.

Lời giải

Đáp án đúng là: D

Dựa vào đồ thị ta có a > 0, đồ thị cắt Oy tại 1 điểm có tung độ dương nên d > 0, đồ thị có 2 cực trị trái dấu nên:

x₁.x₂ < 0 \( \Rightarrow \frac{c}{a} < 0\) ⇒ c < 0

Câu 3

Rút gọn biểu thức \(Q = {b^{\frac{5}{3}}}:\sqrt[3]{b}\) với b > 0

A. Q = b²;

B. \(Q = {b^{\frac{5}{9}}}\);

C. \(Q = {b^{ - \frac{4}{3}}}\);

D. \(Q = {b^{\frac{4}{3}}}\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Tập nghiệm của bất phương trình \({\left( {\frac{2}{3}} \right)^x} > 0\) là

A. (−∞; 0);

B. (1; + ∞);

C. (0; 1);

D. ℝ.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho hình nó (N) có đỉnh S, bán kính đáy bằng a và độ dài đường sinh bằng 4a. Gọi (T) là mặt cầu đi qua S và đường tròn đáy của (N). Bán kính của (T) bằng:

A. \(\frac{{2\sqrt 6 a}}{3}\);

B. \(\frac{{16\sqrt {15} a}}{{15}}\);

C. \(\frac{{8\sqrt {15} a}}{{15}}\);

D. \(\sqrt {15} a\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho hàm số y = x⁴ + 8x² + m có giá trị nhỏ nhất trên [1; 3] bằng 6. Tham số thực m bằng

A. −42;

B. 6;

C. 15;

D. −3.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Cho hệ phương trình \[\left\{ \begin{array}{l}\left( {m - 1} \right)x + y = 2\\mx + y = m + 1\end{array} \right.\] với m là tham số.

Chứng minh rằng với mọi giá trị của m thì hệ phương trình luôn có nghiệm duy nhất (x; y) thỏa mãn 2x + y ≤ 3.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Bình luận

Cho hình chóp S.ABC, gọi G là trọng tâm tam giác ABC. Tìm mệnh đề đúng trong các mệnh đề sau:

Cho hàm số y = ax3 + bx2 + cx + d (a ≠ 0) có đồ thị nhứ hình vẽ dưới đây. Chọn khẳng định đúng về dấu của a, b, c, d.

Rút gọn biểu thức \(Q = {b^{\frac{5}{3}}}:\sqrt[3]{b}\) với b > 0

Tập nghiệm của bất phương trình \({\left( {\frac{2}{3}} \right)^x} > 0\) là

Cho hình nó (N) có đỉnh S, bán kính đáy bằng a và độ dài đường sinh bằng 4a. Gọi (T) là mặt cầu đi qua S và đường tròn đáy của (N). Bán kính của (T) bằng:

Cho hàm số y = x4 + 8x2 + m có giá trị nhỏ nhất trên [1; 3] bằng 6. Tham số thực m bằng

Cho hệ phương trình \[\left\{ \begin{array}{l}\left( {m - 1} \right)x + y = 2\\mx + y = m + 1\end{array} \right.\] với m là tham số. Chứng minh rằng với mọi giá trị của m thì hệ phương trình luôn có nghiệm duy nhất (x; y) thỏa mãn 2x + y ≤ 3.

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho hàm số y = ax³ + bx² + cx + d (a ≠ 0) có đồ thị nhứ hình vẽ dưới đây. Chọn khẳng định đúng về dấu của a, b, c, d.

Cho hàm số y = x⁴ + 8x² + m có giá trị nhỏ nhất trên [1; 3] bằng 6. Tham số thực m bằng

Cho hệ phương trình \[\left\{ \begin{array}{l}\left( {m - 1} \right)x + y = 2\\mx + y = m + 1\end{array} \right.\] với m là tham số.

Chứng minh rằng với mọi giá trị của m thì hệ phương trình luôn có nghiệm duy nhất (x; y) thỏa mãn 2x + y ≤ 3.