Gọi A, B lần lượt là điểm cực đại và điểm cực tiểu của đồ thị hàm số y = x3 − 3x2 + 2. Trung điểm I của đoạn thẳng AB có tọa độ nào dưới đây? A. (1; 1); B. (2; 0); C. (1; 0); D. (1; −2).

Câu hỏi:

24/08/2023 5,233

Gọi A, B lần lượt là điểm cực đại và điểm cực tiểu của đồ thị hàm số y = x³ − 3x² + 2. Trung điểm I của đoạn thẳng AB có tọa độ nào dưới đây?

A. (1; 1);

B. (2; 0);

C. (1; 0);

D. (1; −2).

Xem lời giải

Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Đáp án đúng là: C

TXĐ: D = ℝ

Ta có: $y^{'} = 3 x^{2} - 6 x = 0 \Leftrightarrow [\begin{array}{l} x = 0 \Rightarrow y = 2 \\ x = 2 \Rightarrow y = - 2 \end{array}$

Mà do hàm số có a = 1 > 0 nên cực tiểu của hàm số là x = 2 và cực đại của hàm số là x = 0.

Suy ra cực đại và điểm cực tiểu của đồ thị hàm số là A(0; 2) và B(2; −2).

Gọi I là trung điểm của đoạn thẳng nối hai điểm cực trị A, B ta có:

$\{\begin{cases} x_{I} = \frac{x_{A} + x_{B}}{2} \\ y_{I} = \frac{y_{A} + y_{B}}{2} \end{cases} \Rightarrow \{\begin{cases} x_{I} = \frac{0 + 2}{2} \\ y_{I} = \frac{2 + (- 2)}{2} \end{cases} \Rightarrow \{\begin{cases} x_{I} = 1 \\ y_{I} = 0 \end{cases}$

Vậy I(1; 0).

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hai hàm số $f (x) = a x^{3} + b x^{2} + c x - \frac{1}{2}$ và g (x) = dx² + ex + 1 (a, b, c, d, e Î ℝ). Biết rằng đồ thị hàm số y = f (x) và y = g (x) cắt nhau tại ba điểm có hoành độ lần lượt là −3; −1; 1 (tham khảo hình vẽ). Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng

Xem đáp án

Lời giải

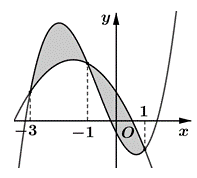
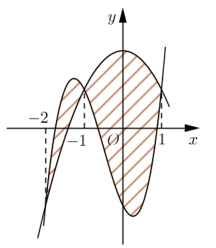
Phương trình hoành độ giao điểm của đồ thị f (x) và g (x) là:

$a x^{3} + b x^{2} + c x - \frac{1}{2} = d x^{2} + e x + 1$

$\Leftrightarrow a x^{3} + (b - d) x^{2} + (c - e) x - \frac{3}{2} = 0 (*)$

Do đồ thị của hai hàm số cắt nhau tại ba điểm suy ra phương trình (*) có ba nghiệm là −3; −1; 1.

Ta được $a (x + 3) (x + 1) (x - 1) = a x^{3} + (b - d) x^{2} + (c - e) x - \frac{3}{2}$

$\Leftrightarrow a (x + 3) (x^{2} - 1) = a x^{3} + (b - d) x^{2} + (c - e) x - \frac{3}{2}$

$\Leftrightarrow a x^{3} + 3 a x^{2} - a x - 3 a = a x^{3} + (b - d) x^{2} + (c - e) x - \frac{3}{2}$

Đồng nhất hai vế ta suy ra:

$\{\begin{cases} 3 a = b - d \\ - a = c - e \\ - 3 a = - \frac{3}{2} \end{cases} \Leftrightarrow \{\begin{cases} a = \frac{1}{2} \\ b - d = \frac{3}{2} \\ c - e = - \frac{1}{2} \end{cases}$

Vậy diện tích hình phẳng cần tìm là

$S = \int_{- 3}^{- 1} (\frac{1}{2} x^{3} + \frac{3}{2} x^{2} - \frac{1}{2} x - \frac{3}{2}) d x + \int_{- 1}^{1} (- \frac{1}{2} x^{3} - \frac{3}{2} x^{2} + \frac{1}{2} x + \frac{3}{2}) d x$

$= {(\frac{x^{4}}{8} + \frac{x^{3}}{2} - \frac{x^{2}}{4} - \frac{3 x}{2})|}_{- 3}^{- 1} + {(- \frac{x^{4}}{8} - \frac{x^{3}}{2} + \frac{x^{2}}{4} + \frac{3 x}{2})|}_{- 1}^{1}$

$= \frac{{(- 1)}^{4}}{8} + \frac{{(- 1)}^{3}}{2} - \frac{{(- 1)}^{2}}{4} - \frac{3 . (- 1)}{2} - \frac{{(- 3)}^{4}}{8} - \frac{{(- 3)}^{3}}{2} + \frac{{(- 3)}^{2}}{4} + \frac{3 . (- 3)}{2}$

$- \frac{1^{4}}{8} - \frac{1^{3}}{2} + \frac{1^{2}}{4} + \frac{3 . 1}{2} + \frac{{(- 1)}^{4}}{8} + \frac{{(- 1)}^{3}}{2} - \frac{{(- 1)}^{2}}{4} - \frac{3 . (- 1)}{2}$

$= \frac{1}{8} - \frac{1}{2} - \frac{1}{4} + \frac{3}{2} - \frac{81}{8} + \frac{27}{2} + \frac{9}{4} - \frac{9}{2} - \frac{1}{8} - \frac{1}{2} + \frac{1}{4} + \frac{3}{2} + \frac{1}{8} - \frac{1}{2} - \frac{1}{4} + \frac{3}{2}$ = 4.

Câu 2

Cho hình chữ nhật ABCD, AB = 3, AD = 4. Hãy tính độ lớn của

a) $\vec{A B} + \vec{A D}$

b) $2 \vec{A B} + 3 \vec{A D}$

Xem đáp án

Lời giải

a) Áp dụng định lí Pytago vào tam giác ABC vuông tại B có:

$A C = \sqrt{A B^{2} + B C^{2}} = \sqrt{3^{2} + 4^{2}} = 5$

$\vec{A B} + \vec{A D} = \vec{A C} \Rightarrow |\vec{A B} + \vec{A D}| = |\vec{A C}| = A C = 5$

b) Đặt $T = |2 \vec{A B} + 3 \vec{A D}|$

$\Rightarrow T^{2} = 4 A B^{2} + 9 A D^{2} + 12 \vec{A B} . \vec{A D} = 4 A B^{2} + 9 A D^{2}$ (Do AB ^ AD)

Þ T² = 4.3² + 9.4² = 180

$\Rightarrow T = 6 \sqrt{5}$

Vậy $T = |2 \vec{A B} + 3 \vec{A D}| = 6 \sqrt{5}$

Câu 3