Lãi suất gửi tiết kiệm của ngân hàng A thời gian vừa qua thay đổi liên tục. Bạn Duy gửi số tiền ban đầu là 10 triệu đồng với lãi suất 0,8% một tháng. Chưa đầy một năm, thì lãi suất tăng lên 1,2% một tháng trong nửa năm tiếp theo. Và bạn Duy tiếp tục gửi; sau nửa năm đó lãi suất giảm xuống còn 1% một tháng. Đồng thời bạn Duy quyết định gửi thêm một số tháng tròn nữa. Biết rằng khi rút tiền bạn Duy được cả vốn lẫn lãi là 12 153 337,95 triệu đồng. Tổng số tháng mà bạn Duy gửi tiết kiệm là:
Lãi suất gửi tiết kiệm của ngân hàng A thời gian vừa qua thay đổi liên tục. Bạn Duy gửi số tiền ban đầu là 10 triệu đồng với lãi suất 0,8% một tháng. Chưa đầy một năm, thì lãi suất tăng lên 1,2% một tháng trong nửa năm tiếp theo. Và bạn Duy tiếp tục gửi; sau nửa năm đó lãi suất giảm xuống còn 1% một tháng. Đồng thời bạn Duy quyết định gửi thêm một số tháng tròn nữa. Biết rằng khi rút tiền bạn Duy được cả vốn lẫn lãi là 12 153 337,95 triệu đồng. Tổng số tháng mà bạn Duy gửi tiết kiệm là:
Quảng cáo
Trả lời:
Gọi x là số tháng gửi với lãi suất 0,8% một tháng (0 < x < 12)
Gọi y là số tháng gửi với lãi suất 1% một tháng
Tổng số tháng mà bạn Duy gửi tiết kiệm là x + 6 + y tháng
Theo giá thiết, ta có:
10.106.(1 + 0,8%)x.(1 + 1,2%)6.(1 + 1%)y = 12153337,95
Û 1,008x.1,01y = 1,131
Lần lượt gán các giá trị của x bằng 1 đến 11 với x là số nguyên ta sẽ tìm được y nguyên khi x = 8, y = 6.
Suy ra tổng số tháng mà bạn Duy gửi tiết kiệm là:
x + 6 + y = 8 + 6 + 6 = 20 tháng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
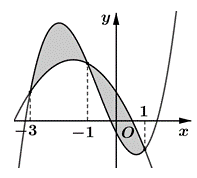
Phương trình hoành độ giao điểm của đồ thị f (x) và g (x) là:
Do đồ thị của hai hàm số cắt nhau tại ba điểm suy ra phương trình (*) có ba nghiệm là −3; −1; 1.
Ta được
Đồng nhất hai vế ta suy ra:
Vậy diện tích hình phẳng cần tìm là
= 4.
Lời giải
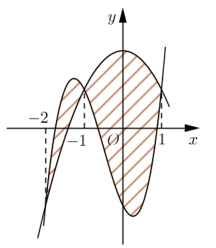
Phương trình hoành độ giao điểm của đồ thị f (x) và g (x) là:
ax3 + bx2 + cx − 2 = dx2 + ex + 2
Û ax3 + (b − d)x2 + (c − e)x − 4 = 0 (1)
Vì phương trình (1) có các nghiệm −2; −1; 1 nên:
Diện tích hình phẳng cần tìm là:
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.