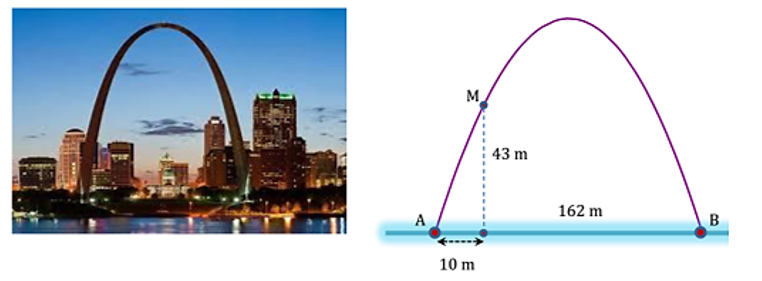
Xác định chiều cao của một tháp mà không cần lên đỉnh của tháp. Đặt kế giác thẳng đứng cách chân tháp một khoảng CD = 60 m, giả sử chiều cao của giác kế là OC = 1 m. Quay thanh giác kế sao cho khi ngắm theo thanh ta nhình thấy đỉnh A của tháp. Đọc trên giác kế số đo của góc . Chiều cao của ngọn tháp gần với giá trị nào sau đây:
Xác định chiều cao của một tháp mà không cần lên đỉnh của tháp. Đặt kế giác thẳng đứng cách chân tháp một khoảng CD = 60 m, giả sử chiều cao của giác kế là OC = 1 m. Quay thanh giác kế sao cho khi ngắm theo thanh ta nhình thấy đỉnh A của tháp. Đọc trên giác kế số đo của góc . Chiều cao của ngọn tháp gần với giá trị nào sau đây:
Quảng cáo
Trả lời:
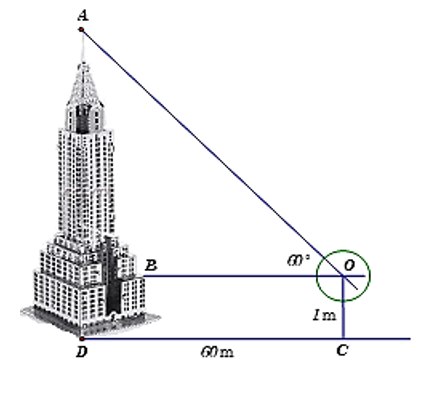
Tam giác OAB vuông tại B, có:
Vậy chiều cao của ngọn tháp là:
Do đó chiều cao của ngọn tháp gần với giá trị 105 m.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có cosx = 1 ⇔ x = k2π (k ∈ ℤ).
Vậy nghiệm của phương trình cosx = 1 là x = k2π (k ∈ ℤ).
Lời giải
Gọi x ≥ 0, y ≥ 0 (tấn) là sản lượng cần sản xuất của sản phẩm A và sản phẩm B.
Ta có:
x + 6y là thời gian hoạt động của máy I.
2x + 3y là thời gian hoạt động của máy II.
3x + 2y là thời gian hoạt động của máy III.
Số tiền lãi của nhà máy: T = 4x + 3y (triệu đồng).
Bài toán trở thành:
Tìm x ≥ 0, y ≥ 0 thỏa mãn để T = 4x + 3y đạt giá trị lớn nhất.
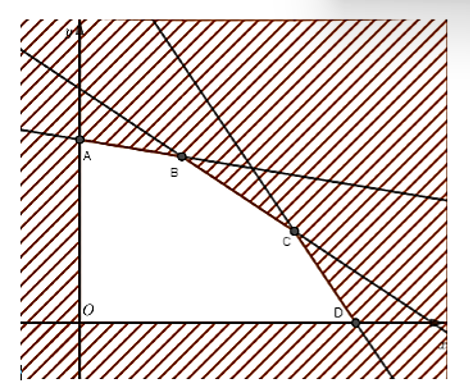
Miền nghiệm của hệ là ngũ giác OABCD, ở đó:
Thay tọa độ các điểm vào biểu thức T ta được Tmax = 36 tại x = 7, y = 3.
Vậy nhà máy nên sản xuất 7 tấn sản phẩm A và 3 tấn sản phẩm B để tiền lãi được nhiều nhất.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.