Trong một trường học, mọi học sinh đều chơi bóng đá hoặc bóng bàn hoặc cả hai. Người ta thấy rằng 200 học sinh chơi bóng đá, 150 học sinh chươi bóng bàn và 100 học sinh chơi cả hai. Tìm xem có bao nhiêu sinh viên trong trường bằng cách sử dụng công thức phép toán tập hợp.
Trong một trường học, mọi học sinh đều chơi bóng đá hoặc bóng bàn hoặc cả hai. Người ta thấy rằng 200 học sinh chơi bóng đá, 150 học sinh chươi bóng bàn và 100 học sinh chơi cả hai. Tìm xem có bao nhiêu sinh viên trong trường bằng cách sử dụng công thức phép toán tập hợp.
Quảng cáo
Trả lời:
Gọi số học sinh chơi bóng đá là n (F) và số học sinh chơi bóng bàn là n (S).
Ta có n (F) = 200, n (S) = 150 và n (F Ç S) = 100.
Ta biết rằng, n (F È S) = n (F) + n (S) − n(F Ç S)
Do đó, n (F È S) = (200 + 150) − 100
n (F È S) = 350 − 100 = 250
Vậy tổng số học sinh toàn trường là 250 em.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có cosx = 1 ⇔ x = k2π (k ∈ ℤ).
Vậy nghiệm của phương trình cosx = 1 là x = k2π (k ∈ ℤ).
Lời giải
Gọi x ≥ 0, y ≥ 0 (tấn) là sản lượng cần sản xuất của sản phẩm A và sản phẩm B.
Ta có:
x + 6y là thời gian hoạt động của máy I.
2x + 3y là thời gian hoạt động của máy II.
3x + 2y là thời gian hoạt động của máy III.
Số tiền lãi của nhà máy: T = 4x + 3y (triệu đồng).
Bài toán trở thành:
Tìm x ≥ 0, y ≥ 0 thỏa mãn để T = 4x + 3y đạt giá trị lớn nhất.
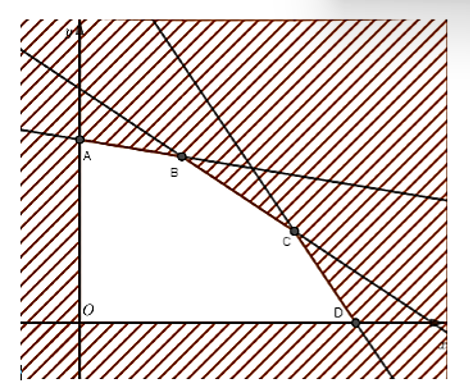
Miền nghiệm của hệ là ngũ giác OABCD, ở đó:
Thay tọa độ các điểm vào biểu thức T ta được Tmax = 36 tại x = 7, y = 3.
Vậy nhà máy nên sản xuất 7 tấn sản phẩm A và 3 tấn sản phẩm B để tiền lãi được nhiều nhất.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.