khoahoc.vietjack.com
Giảm 50% Kích hoạt VIP
khoahoc.vietjack.com
Vào học
Đăng nhập
Tạo VIP
Xin chào! Vào học
  2. Lớp 12
  3. Toán

Câu hỏi:

19/08/2025 3,095 Lưu

Một công ty cần thuê xe vận chuyển 140 người và 9 tấn hàng hóa. Nơi cho thuê xe chỉ có 10 xe hiệu MITSUBISHI và 9 xe hiệu FORD. Một chiếc xe hiệu MITSUBISHI có thể chở 20 người và 0,6 tấn hàng. Một chiếc xe hiệu FORD có thể chở 10 người vfa 1,5 tấn hàng. Tiền thuê một xe hiệu MITSUBISHI là 4 triệu đồng, một xe hiệu FORD là 3 triệu đồng. Hỏi phải thuê bao nhiêu xe mỗi loại để chi phí thấp nhất?

Xem lời giải

Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!

Flashcard Bắt Đầu Thi Giao bài

Quảng cáo

Trả lời:

verified Giải bởi Vietjack
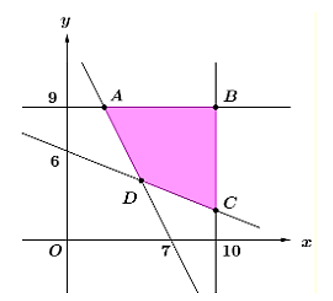
Một công ty cần thuê xe vận chuyển 140 người và 9 tấn hàng hóa. Nơi cho thuê xe chỉ có 10 xe hiệu MITSUBISHI và 9 xe hiệu FORD. Một chiếc xe hiệu MITSUBISHI có thể chở 20 người và 0,6 tấn hàng. Một chiếc xe hiệu FORD có thể chở 10 người vfa 1,5 tấn hàng. Tiền thuê một xe hiệu MITSUBISHI là 4 triệu đồng, một xe hiệu FORD là 3 triệu đồng. Hỏi phải thuê bao nhiêu xe mỗi loại để chi phí thấp nhất? (ảnh 1)

Gọi x, y lần lượt là số xe loại MITSUBISHI, loại FORD cần thuê. ĐK: x, y Î ℕ.

Ta có hệ bất phương trình sau:  0≤x≤100≤y≤920x+10y≥1400,6x+1,5y≥9⇔0≤x≤100≤y≤92x+y≥142x+5y≥30 *

Tổng chi phí T (x; y) = 4x + 3y (triệu đồng)

Bài toán trở thành là tìm x; y nguyên không âm thoả mãn hệ (*) sao cho T (x; y) nhỏ nhất.

Miền nghiệm của hệ trên là tứ giác ABCD.

Ta có:  A52; 9; B10; 9; C10; 2, D5; 4

Ta thấy T đạt GTLN tại các điểm B, C, D (do A có tọa độ không nguyên).

Ta tính được: T (B) = 67, T (C) = 46, T (D) = 32

Vậy chi phí thấp nhất là 32 triệu đồng.

Đang tải chế độ Học...

Hot: 1000+ đề thi cuối kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

  • Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
  • Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
  • Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
  • Tải xuống đề thi [DOCX] với đầy đủ đáp án
  • Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
  • Bao gồm tất cả các bậc từ Tiểu học đến Đại học
  • Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
  • Đăng ký ngay
Avatar

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

. Tìm nghiệm của phương trình cos x = 1.

Lời giải

Ta có cosx = 1 ⇔ x = k2π (k ∈ ℤ).

Vậy nghiệm của phương trình cosx = 1 là x = k2π (k ∈ ℤ).

Câu 2

Một nhà máy sản xuất, sử dụng ba loại máy đặc chủng để sản xuất sản phẩm A và sản phẩm B trong một chu trình sản xuất. Để sản xuất một tấn sản phẩm A lãi 4 triệu đồng người ta sử dụng máy I trong 1 giờ, máy II trong 2 giờ và máy III trong 3 giờ. Để sản xuất ra một tấn sản phẩm B lãi được 3 triệu đồng người ta sử dụng máy I trong 6 giờ, máy II trong 3 giờ và máy III trong 2 giờ. Biết rằng máy I chỉ hoạt động không quá 36 giờ, máy hai hoạt động không quá 23 giờ và máy III hoạt động không quá 27 giờ. Hãy lập kế hoạch sản xuất cho nhà máy để tiền lãi được nhiều nhất.

Lời giải

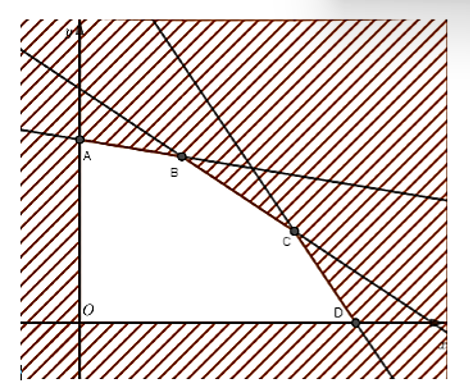
Một nhà máy sản xuất, sử dụng ba loại máy đặc chủng để sản xuất sản phẩm A và sản phẩm B trong một chu trình sản xuất. Để sản xuất một tấn sản phẩm A lãi 4 triệu đồng người ta sử dụng máy I trong 1 giờ, máy II trong 2 giờ và máy III trong 3 giờ. Để sản xuất ra một tấn sản phẩm B lãi được 3 triệu đồng người ta sử dụng máy I trong 6 giờ, máy II trong 3 giờ và máy III trong 2 giờ. Biết rằng máy I chỉ hoạt động không quá 36 giờ, máy hai hoạt động không quá 23 giờ và máy III hoạt động không quá 27 giờ. Hãy lập kế hoạch sản xuất cho nhà máy để tiền lãi được nhiều nhất. (ảnh 1)

Gọi x ≥ 0, y ≥ 0 (tấn) là sản lượng cần sản xuất của sản phẩm A và sản phẩm B. 

Ta có:

x + 6y là thời gian hoạt động của máy I.

2x + 3y là thời gian hoạt động của máy II.

3x + 2y là thời gian hoạt động của máy III.

Số tiền lãi của nhà máy: T = 4x + 3y (triệu đồng).

Bài toán trở thành:

Tìm x ≥ 0, y ≥ 0 thỏa mãn  x+6y≤362x+3y≤233x+2y≤27 để T = 4x + 3y đạt giá trị lớn nhất.

 

Miền nghiệm của hệ là ngũ giác OABCD, ở đó:

 O0; 0, A0; 6, B103; 499, C7; 3, D9; 0

Thay tọa độ các điểm vào biểu thức T ta được Tmax = 36 tại x = 7, y = 3.

Vậy nhà máy nên sản xuất 7 tấn sản phẩm A và 3 tấn sản phẩm B để tiền lãi được nhiều nhất.

Câu 3

Bạn An kinh doanh hai mặt hàng handmade là vòng tay và vòng đeo cổ. Mỗi vòng tay làm trong 4 giờ, bán được 40 ngàn đồng. Mỗi vòng đeo cổ làm trong 6 giờ, bán được 80 ngàn đồng. Mỗi tuần bạn An bán được không quá 15 vòng tay và 4 vòng đeo cổ. Tính số giờ tối thiểu trong tuần An cần dùng để bán được ít nhất 400 ngàn đồng.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Tìm giá trị nhỏ nhất của biểu thức F = y − x trên miền xác định bởi hệ  2x+y≤2x−y≤25x+y≥−4.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Vẽ sơ đồ tư duy khái niệm vectơ.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cổng Arch tại thành phố St Louis của Mỹ có hình dạng là một parabol (hình vẽ). Biết khoảng cách giữa hai chân cổng bằng 162 m. Trên thành cổng, tại vị trí có độ cao 43 m so với mặt đất (điểm M), người ta thả một sợi dây chạm đất (dây căng thẳng theo phương vuông góc với đất). Vị trí chạm đất của đầu sợi dây này cách chân cổng A một đoạn 10 m. Giả sử các số liệu trên là chính xác. Hãy tính độ cao của cổng Arch (tính từ mặt đất đến điểm cao nhất của cổng).

Cổng Arch tại thành phố St Louis của Mỹ có hình dạng là một parabol (hình vẽ). Biết khoảng cách giữa hai chân cổng bằng 162 m. Trên thành cổng, tại vị trí có độ cao 43 m so với mặt đất (điểm M), người ta thả một sợi dây chạm đất (dây căng thẳng theo phương vuông góc với đất). (ảnh 1)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Một của hàng buôn giày nhập một đôi với giá là 40 USD. Cửa hàng ước tính rằng nếu đôi giày được bán với giá x USD thì mỗi tháng khách hàng sẽ mua (120 − x) đôi. Hỏi cửa hàng bán một đôi giày giá bao nhiêu thì thu được nhiều lãi nhất?

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Đăng ký

Bạn đã có tài khoản?

Khóa học 1 - 12
THPT
THCS
Phòng luyện đề
ĐGNL - ĐGTD
Tốt nghiệp THPT
Ôn vào 10
Ôn vào 6
Tài liệu
THPT
THCS
Tin Tuyển Sinh
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack37. All Rights Reserved.
zalo Nhắn tin Zalo Hỏi bài tập