Cho đường tròn (C) có phương trình x2 + y2 − 4x + 6y − 12 = 0. Chứng minh rằng điểm M(5; 1) thuộc (C). Viết phương trình tiếp tuyến d của (C) tại M.
Cho đường tròn (C) có phương trình x2 + y2 − 4x + 6y − 12 = 0. Chứng minh rằng điểm M(5; 1) thuộc (C). Viết phương trình tiếp tuyến d của (C) tại M.
Quảng cáo
Trả lời:
C): x2 + y2 − 4x + 6y − 12 = 0
Û (x2 − 4x + 4) + (y2 + 6y + 9) = 25
Û (x − 2)2 + (y + 3)2 = 25
Suy ra đường tròn (C) có tâm là I(2; −3)
Thay toạ độ điểm M vào phương trình của đường tròn (C) ta có:
52 + 12 − 4.5 + 6.1 − 12 = 0 (luôn đúng)
Do đó điểm M thuộc đường tròn (C).
Tiếp tuyến d của (C) tại điểm M là đường thẳng đi qua M và vuông góc với IM nên có một vectơ pháp tuyến là
Vậy phương trình của tiếp tuyến d là:
3(x − 5) + 4(y − 1) = 0
Û 3x + 4y − 19 = 0.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có cosx = 1 ⇔ x = k2π (k ∈ ℤ).
Vậy nghiệm của phương trình cosx = 1 là x = k2π (k ∈ ℤ).
Lời giải
Gọi x ≥ 0, y ≥ 0 (tấn) là sản lượng cần sản xuất của sản phẩm A và sản phẩm B.
Ta có:
x + 6y là thời gian hoạt động của máy I.
2x + 3y là thời gian hoạt động của máy II.
3x + 2y là thời gian hoạt động của máy III.
Số tiền lãi của nhà máy: T = 4x + 3y (triệu đồng).
Bài toán trở thành:
Tìm x ≥ 0, y ≥ 0 thỏa mãn để T = 4x + 3y đạt giá trị lớn nhất.
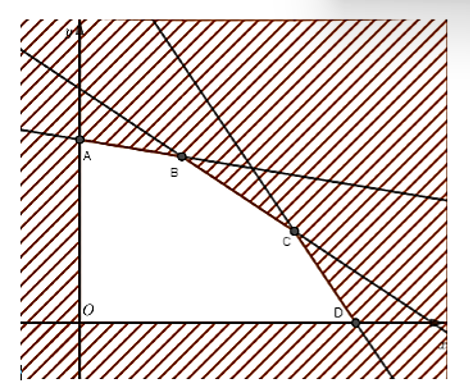
Miền nghiệm của hệ là ngũ giác OABCD, ở đó:
Thay tọa độ các điểm vào biểu thức T ta được Tmax = 36 tại x = 7, y = 3.
Vậy nhà máy nên sản xuất 7 tấn sản phẩm A và 3 tấn sản phẩm B để tiền lãi được nhiều nhất.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.