Câu hỏi:

15/09/2023 96,365

Lớp 10A có 7 học sinh giỏi Toán, 5 học sinh giỏi Lý, 6 học sinh giỏi Hóa, 3 học sinh giỏi cả Toán và Lý, 4 học sinh giỏi cả Toán và Hoá, 2 học sinh giỏi cả Lý và Hóa, 1 học sinh giỏi cả ba môn Toán, Lý, Hóa. Số học sinh giỏi ít nhất một môn (Toán, Lý, Hóa) của lớp 10A là

A. 9.

B. 18.

C. 10.

D. 28.

Xem lời giải

Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

Đáp án đúng là: C

Lớp 10A có 7 học sinh giỏi Toán, 5 học sinh giỏi Lý, 6 học sinh giỏi Hóa, 3 học sinh giỏi cả Toán và Lý, 4 học sinh giỏi cả Toán và Hoá, 2 học sinh giỏi cả Lý và Hóa, 1 học sinh giỏi cả ba môn Toán, Lý, Hóa. Số học sinh giỏi ít nhất một môn (Toán, Lý, Hóa) của lớp 10A là A. 9. B. 18. C. 10. D. 28. (ảnh 1)

Số học sinh giỏi toán, lý mà không giỏi hóa: 3 – 1 = 2.

Số học sinh giỏi toán, hóa mà không giỏi lý: 4 – 1 = 3.

Số học sinh giỏi hóa, lý mà không giỏi toán: 2 – 1 = 1.

Số học sinh chỉ giỏi môn lý: 5 – 2 – 1 – 1 = 1.

Số học sinh chỉ giỏi môn hóa: 6 – 3 – 1 – 1 = 1.

Số học sinh chỉ giỏi môn toán: 7 – 3 – 2 – 1 = 1.

Số học sinh giỏi ít nhất một (môn toán, lý, hóa) là số học sinh giỏi 1 môn hoặc 2 môn hoặc cả 3 môn: 1 + 1 + 1 + 1 + 2 + 3 + 1 = 10.

Đang tải chế độ Học...

Hot: 1000+ đề thi cuối kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
Đăng ký ngay

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một doanh nghiệp tư nhân A chuyên kinh doanh xe gắn máy các loại. Hiện nay doanh nghiệp đang tập trung chiến lược vào kinh doanh xe hon đa Future Fi với chi phí mua vào một chiếc là 27 (triệu đồng) và bán ra với giá là 31 triệu đồng. Với giá bán này thì số lượng xe mà khách hàng sẽ mua trong một năm là 600 chiếc. Nhằm mục tiêu đẩy mạnh hơn nữa lượng tiêu thụ dòng xe đang ăn khách này, doanh nghiệp dự định giảm giá bán và ước tính rằng nếu giảm 1 triệu đồng mỗi chiếc xe thì số lượng xe bán ra trong một năm là sẽ tăng thêm 200 chiếc. Vậy doanh nghiệp phải định giá bán mới là bao nhiêu để sau khi đã thực hiện giảm giá, lợi nhuận thu được sẽ là cao nhất.

Xem đáp án

Lời giải

Gọi x (triệu) đồng là số tiền mà doanh nghiệp A dự định giảm giá (0 ≤ x ≤ 4).

Khi đó:

Lợi nhuận thu được khi bán một chiếc xe là 31 – x – 27 = 4 – x (triệu đồng).

Số xe mà doanh nghiệp sẽ bán được trong một năm là 600 + 200x (chiếc).

Lợi nhuận mà doanh nghiệp thu được trong một năm là

f(x) = (4 − x)(600 + 200x) = −200x² + 200x + 2400.

Xét hàm số f(x) = −200x² + 200x + 2400 trên đoạn [0; 4] có bảng biến thiên:

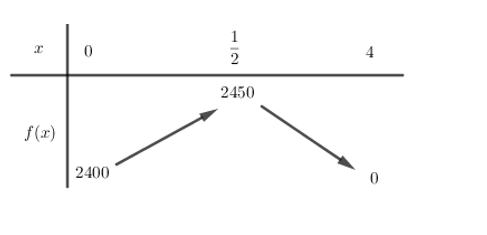
Một doanh nghiệp tư nhân A chuyên kinh doanh xe gắn máy các loại. Hiện nay doanh nghiệp đang tập trung chiến lược vào kinh doanh xe hon đa Future Fi với chi phí mua vào một chiếc là 27 (triệu đồng) và bán ra với giá là 31 triệu đồng. Với giá bán này thì số lượng xe mà khách hàng sẽ mua trong một năm là 600 chiếc. Nhằm mục tiêu đẩy mạnh hơn nữa lượng tiêu thụ dòng xe đang ăn khách này, doanh nghiệp dự định giảm giá bán và ước tính rằng nếu giảm 1 triệu đồng mỗi chiếc xe thì số lượng xe bán ra trong một năm là sẽ tăng thêm 200 chiếc. (ảnh 1)

Vậy $\max_{[0; 4]} f (x) = 2 450$ ⇔ $x = \frac{1}{2} .$

Vậy giá mới của chiếc xe là 30,5 triệu đồng thì lợi nhuận thu được là cao nhất.

Câu 2

Cho hình chóp S.ABCD có đáy ABCD là hình thang có cạnh đáy AB và CD. Gọi I, J lần lượt là trung điểm của các cạnh AD và BC và G là trọng tâm tam giác SAB. Tìm điều kiện của AB và CD để thiết diện của (IJG) và hình chóp là một hình bình hành.

Xem đáp án

Lời giải

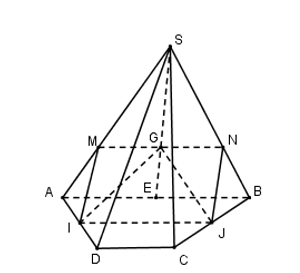
Cho hình chóp S.ABCD có đáy ABCD là hình thang có cạnh đáy AB và CD. Gọi I, J lần lượt là trung điểm của các cạnh AD và BC và G là trọng tâm tam giác SAB. Tìm điều kiện của AB và CD để thiết diện của (IJG) và hình chóp là một hình bình hành. (ảnh 1)

Ta có: ABCD là hình thang và I, J là trung điểm của AD và BC nên IJ là đường trung bình của hình thang ABCD.

⇒ IJ // AB // CD.

$\{\begin{matrix} G \in (S A B) \cap (I J G) \\ A B \subset (S A B) \\ I J \subset (I J G) \\ A B ∥ I J \end{matrix}$

⇒ Trong (SAB) qua G kẻ MN // AB (M ∈ SA; N ∈ SB)

⇒ (SAB) ∩ (IJG) = MN và MN // IJ // AB // CD.

Dễ thấy thiết diện của (IJG) và hình chóp là hình thang MNJI.

G là trọng tâm của tam giác SAB và MN // AB nên theo định lí Ta-let ta có:

$\frac{M N}{A B} = \frac{S G}{S E} = \frac{2}{3}$ (với E là trung điểm của AB).

⇒ $M N = \frac{2}{3} A B$ .

Lại có: IJ là đường trung bình của hình thang ABCD nên $I J = \frac{A B + C D}{2} .$

Để hình thang MNJI trở thành hình bình hành thì cần điều kiện MN = IJ.

⇒ $\frac{2}{3} A B = \frac{1}{2} (A B + C D)$ ⇔ $\frac{1}{6} A B = \frac{1}{2} C D$ ⇔ $A B = 3 C D .$

Câu 3

Một công ty Y cần thuê xe để chở 140 người và 9 tấn hàng. Nơi thuê xe có 2 loại xe, trong đó có 10 xe loại A và 9 xe loại B. Một chiếc xe loại A cho thuê với giá 4 triệu, một chiếc xe loại B cho thuê với giá 3 triệu. Biết rằng mỗi xe loại A có thể chở 20 người và 0,6 tấn hàng; mỗi xe loại B có thể chở tối đa 10 người và 1,5 tấn. Công ty Y cần thuê bao nhiêu xe mỗi loại để chi phí bỏ ra ít nhất?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho hàm số f(x) có bảng biến thiên như sau:

Số nghiệm thuộc đoạn [-π; 2π] của phương trình 2f(sin x) + 3 = 0 là:

A. 4.

B. 6.

C. 3.

D. 8.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho tam giác ABC với H, O, G lần lượt là trực tâm, tâm đường tròn ngoại tiếp, trọng tâm của tam giác. Hệ thức đúng là:

A. $\vec{O H} = \frac{3}{2} \vec{O G} .$

B. $\vec{H O} = 3 \vec{O G} .$

C. $\vec{O G} = \frac{1}{2} \vec{G H} .$

D. $2 \vec{G O} = - 3 \vec{O H} .$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho bốn điểm không đồng phẳng, ta có thể xác định được nhiều nhất bao nhiêu mặt phẳng phân biệt từ bốn điểm đã cho?

A. 2.

B. 3.

C. 4.

D. 6.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

Đại học

ĐGNL - ĐGTD

Tốt nghiệp THPT

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

V-ACT

HSA

TSA

SPT

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Cho hàm số f(x) có bảng biến thiên như sau:

Số nghiệm thuộc đoạn [-π; 2π] của phương trình 2f(sin x) + 3 = 0 là: