Cho hàm số f(x) có bảng biến thiên như sau:
![Cho hàm số f(x) có bảng biến thiên như sau: Số nghiệm thuộc đoạn [π; 2π] của phương trình 2f(sin x) + 3 = 0 là: A. 4. B. 6. C. 3. D. 8. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/09/blobid5-1694745831.png)
Số nghiệm thuộc đoạn [-π; 2π] của phương trình 2f(sin x) + 3 = 0 là:
Cho hàm số f(x) có bảng biến thiên như sau:
![Cho hàm số f(x) có bảng biến thiên như sau: Số nghiệm thuộc đoạn [π; 2π] của phương trình 2f(sin x) + 3 = 0 là: A. 4. B. 6. C. 3. D. 8. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/09/blobid5-1694745831.png)
Số nghiệm thuộc đoạn [-π; 2π] của phương trình 2f(sin x) + 3 = 0 là:
Quảng cáo
Trả lời:
Đáp án đúng là: B
Phương trình ⇔ (*) có nghiệm trên [-π; 2π]
⇔ đường thẳng cắt đồ thị hàm số y = f(sin x) tại các điểm trên [-π; 2π].
Đặt sin x = t ⇒ x ∈ [-π; 2π] ⇒ t ∈ [-1; 1].
Ta có bảng biến thiên:
![Cho hàm số f(x) có bảng biến thiên như sau: Số nghiệm thuộc đoạn [π; 2π] của phương trình 2f(sin x) + 3 = 0 là: A. 4. B. 6. C. 3. D. 8. (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2023/09/blobid6-1694745883.png)
Ta có (*) ⇔
![Cho hàm số f(x) có bảng biến thiên như sau: Số nghiệm thuộc đoạn [π; 2π] của phương trình 2f(sin x) + 3 = 0 là: A. 4. B. 6. C. 3. D. 8. (ảnh 3)](https://video.vietjack.com/upload2/quiz_source1/2023/09/blobid7-1694745952.png)
Dựa vào đồ thị hàm số ta thấy:
• Đường thẳng y = t1 cắt đồ thị hàm số y = sin x tại hai điểm phân biệt trong [-π; 2π].
• Đường thẳng y = t2 cắt đồ thị hàm số y = sin x tại bốn điểm phân biệt trong [-π; 2π].
Như vậy đường thẳng cắt đồ thị hàm số y = f(sin x) tại 6 điểm phân biệt trên [-π; 2π].
Vậy phương trình đã cho có 6 nghiệm phân biệt.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Đáp án đúng là: C

Số học sinh giỏi toán, lý mà không giỏi hóa: 3 – 1 = 2.
Số học sinh giỏi toán, hóa mà không giỏi lý: 4 – 1 = 3.
Số học sinh giỏi hóa, lý mà không giỏi toán: 2 – 1 = 1.
Số học sinh chỉ giỏi môn lý: 5 – 2 – 1 – 1 = 1.
Số học sinh chỉ giỏi môn hóa: 6 – 3 – 1 – 1 = 1.
Số học sinh chỉ giỏi môn toán: 7 – 3 – 2 – 1 = 1.
Số học sinh giỏi ít nhất một (môn toán, lý, hóa) là số học sinh giỏi 1 môn hoặc 2 môn hoặc cả 3 môn: 1 + 1 + 1 + 1 + 2 + 3 + 1 = 10.
Lời giải
Gọi x (triệu) đồng là số tiền mà doanh nghiệp A dự định giảm giá (0 ≤ x ≤ 4).
Khi đó:
Lợi nhuận thu được khi bán một chiếc xe là 31 – x – 27 = 4 – x (triệu đồng).
Số xe mà doanh nghiệp sẽ bán được trong một năm là 600 + 200x (chiếc).
Lợi nhuận mà doanh nghiệp thu được trong một năm là
f(x) = (4 − x)(600 + 200x) = −200x2 + 200x + 2400.
Xét hàm số f(x) = −200x2 + 200x + 2400 trên đoạn [0; 4] có bảng biến thiên:
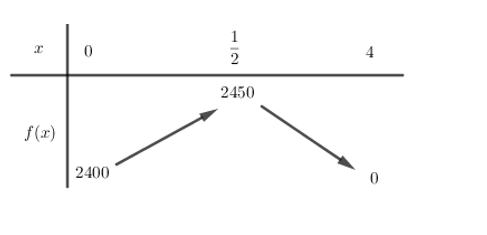
Vậy ⇔
Vậy giá mới của chiếc xe là 30,5 triệu đồng thì lợi nhuận thu được là cao nhất.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.