Câu hỏi:
15/09/2023 1,630
Cho tam giác ABC có G là trọng tâm. Gọi H là chân đường cao hạ từ A sao cho \(\overrightarrow {BH} = \frac{1}{3}\overrightarrow {HC} \). Điểm M di động trên BC sao cho \(\overrightarrow {BM} = x.\overrightarrow {BC} \). Tìm x sao cho độ dài vectơ \(\left| {\overrightarrow {MA} + \overrightarrow {GC} } \right|\) đạt giá trị nhỏ nhất.
Cho tam giác ABC có G là trọng tâm. Gọi H là chân đường cao hạ từ A sao cho \(\overrightarrow {BH} = \frac{1}{3}\overrightarrow {HC} \). Điểm M di động trên BC sao cho \(\overrightarrow {BM} = x.\overrightarrow {BC} \). Tìm x sao cho độ dài vectơ \(\left| {\overrightarrow {MA} + \overrightarrow {GC} } \right|\) đạt giá trị nhỏ nhất.
Đáp án chính xác
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: B
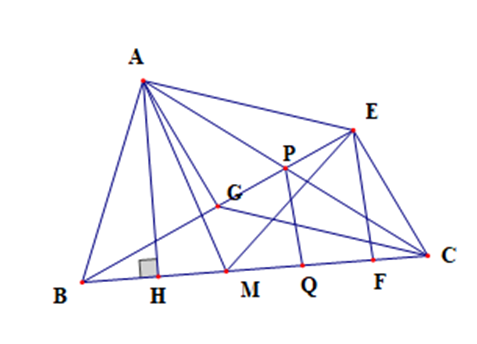
Dựng hình bình hành AGCE. Ta có
\(\overrightarrow {MA} + \overrightarrow {GC} = \overrightarrow {MA} + \overrightarrow {AE} = \overrightarrow {ME} \)
Kẻ \(EF \bot BC,F \in BC \Rightarrow |\overrightarrow {MA} + \overrightarrow {GC} | = |ME| \ge EF\)
Do đó: \(\left| {\overrightarrow {MA} + \overrightarrow {GC} } \right|\) nhỏ nhất khi M ≡ F
Gọi P là trung điểm AC, Q là hình chiếu của P trên BC
Ta có: \(BP = 3PG = \frac{3}{4}BE\)
Vì \(\left\{ \begin{array}{l}PQ \bot BC\\F{\rm{E}} \bot BC\end{array} \right. \Rightarrow PQ//F{\rm{E}}\) nên \(\widehat {BQP} = \widehat {BF{\rm{E}}}\) (hai góc đồng vị)
Xét ∆BPQ và ∆BEF có:
\(\widehat {EBF}\) là góc chung
\(\widehat {BQP} = \widehat {BF{\rm{E}}}\) (chứng minh trên)
Do đó (g.g)
\( \Rightarrow \frac{{BQ}}{{BF}} = \frac{{BP}}{{BE}} = \frac{3}{4} \Rightarrow \overrightarrow {BF} = \frac{4}{3}\overrightarrow {BQ} \)
Mặt khác: \(\overrightarrow {BH} = \frac{1}{3}\overrightarrow {HC} \) nên PQ là đường trung bình của tam giác AHC
Suy ra \(\overrightarrow {HQ} = \frac{1}{2}\overrightarrow {HC} \)
Ta có:
\(\overrightarrow {BQ} = \overrightarrow {BH} + \overrightarrow {HQ} = \frac{1}{3}\overrightarrow {HC} + \frac{1}{2}\overrightarrow {HC} = \frac{5}{6}\overrightarrow {HC} = \frac{5}{8}\overrightarrow {BC} \Rightarrow \overrightarrow {BF} = \frac{4}{3}\overrightarrow {BQ} = \frac{5}{6}\overrightarrow {BC} \Rightarrow x = \frac{5}{6}\)
Vậy ta chọn đáp án B.
Sách thầy cô Vietjack biên soạn
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Có 6 chiếc ghế được kê thành một hàng ngang. Xếp ngẫu nhiên 6 học sinh, gồm 3 học sinh lớp A, 2 học sinh lớp B và 1 học sinh lớp C, ngồi vào hàng ghế đó, sao cho mỗi ghế có đúng một học sinh. Xác suất để học sinh lớp C chỉ ngồi cạnh học sinh lớp B bằng
Có 6 chiếc ghế được kê thành một hàng ngang. Xếp ngẫu nhiên 6 học sinh, gồm 3 học sinh lớp A, 2 học sinh lớp B và 1 học sinh lớp C, ngồi vào hàng ghế đó, sao cho mỗi ghế có đúng một học sinh. Xác suất để học sinh lớp C chỉ ngồi cạnh học sinh lớp B bằng
Xem đáp án »
18/09/2023
50,573
Câu 2:
Phương trình \({\left( {\sqrt 5 } \right)^{{x^2} + 4{\rm{x}} + 6}} = {\log _2}128\) có bao nhiêu nghiệm?
Phương trình \({\left( {\sqrt 5 } \right)^{{x^2} + 4{\rm{x}} + 6}} = {\log _2}128\) có bao nhiêu nghiệm?
Xem đáp án »
18/09/2023
18,631
Câu 3:
Người ta sử dụng 7 cuốn sách Toán, 8 cuốn sách Vật lí, 9 cuốn sách Hóa học (các cuốn sách cùng loại giống nhau) để làm phần thưởng cho 12 học sinh, mỗi học sinh được 2 cuốn sách khác loại. Trong số 12 học sinh trên có hai bạn Tâm và Huy. Tính xác suất để hai bạn Tâm và Huy có phần thưởng giống nhau.
Người ta sử dụng 7 cuốn sách Toán, 8 cuốn sách Vật lí, 9 cuốn sách Hóa học (các cuốn sách cùng loại giống nhau) để làm phần thưởng cho 12 học sinh, mỗi học sinh được 2 cuốn sách khác loại. Trong số 12 học sinh trên có hai bạn Tâm và Huy. Tính xác suất để hai bạn Tâm và Huy có phần thưởng giống nhau.
Xem đáp án »
18/09/2023
15,933
Câu 4:
Gieo đồng tiền hai lần. Số phần tử của biến cố để mặt ngửa xuất hiện đúng 1 lần là:
Xem đáp án »
18/09/2023
10,093
Câu 5:
Tập xác định của hàm số \(f\left( x \right) = {\left( {9{{\rm{x}}^2} - 25} \right)^{ - 2}} + {\log _2}\left( {2{\rm{x}} + 1} \right)\) là:
Tập xác định của hàm số \(f\left( x \right) = {\left( {9{{\rm{x}}^2} - 25} \right)^{ - 2}} + {\log _2}\left( {2{\rm{x}} + 1} \right)\) là:
Xem đáp án »
18/09/2023
6,511
Câu 6:
Tìm tất cả các giá trị thực của tham số m để phương trình 3x = m có nghiệm thực:
Tìm tất cả các giá trị thực của tham số m để phương trình 3x = m có nghiệm thực:
Xem đáp án »
18/09/2023
6,283
Câu 7:
Có bao nhiêu giá trị nguyên dương của m để hàm số y = ln(x3 – 3m2x + 72m) xác định trên (0; +∞).
Có bao nhiêu giá trị nguyên dương của m để hàm số y = ln(x3 – 3m2x + 72m) xác định trên (0; +∞).
Xem đáp án »
15/09/2023
5,106
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
80 câu Bài tập Hình học Khối đa diện có lời giải chi tiết (P1)
-
148 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu từ đề thi Đại học có lời giải (P1)
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)
-
62 câu Trắc nghiệm Khái niệm về khối đa diện (nhận biết)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận