Câu hỏi:

18/09/2023 675

Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 24g hương liệu, 9 lít nước và 210g đường để pha chế nước cam và nước táo.

+ Để pha chế 1 lít nước cam cần 30g đường, 1 lít nước và 1g hương liệu;

+ Để pha chế 1 lít nước táo cần 10g đường, 1 lít nước và 4g hương liệu.

Mỗi lít nước cam nhận được 60 điểm thưởng, mỗi lít nước táo nhận được 80 điểm thưởng. Hỏi cần pha chế bao nhiêu lít nước trái cây mỗi loại để đạt được số điểm thưởng cao nhất?

A. 5 lít nước cam và 4 lít nước táo.

B. 6 lít nước cam và 5 lít nước táo.

C. 4 lít nước cam và 5 lít nước táo.

D. 4 lít nước cam và 6 lít nước táo.

Xem lời giải

Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Đáp án đúng là: C

Giả sử x, y lần lượt là số lít nước cam và số lít nước táo mà mỗi đội cần pha chế.

Suy ra 30x + 10y là số gam đường cần dùng;

x + y là số lít nước cần dùng;

x + 4y là số gam hương liệu cần dùng.

Theo giả thiết ta có: \(\left\{ {\begin{array}{*{20}{c}}{x \ge 0}\\{y \ge 0}\\{30x + 10y \le 210}\\{x + y \le 9}\\{x + 4y \le 24}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x \ge 0}\\{y \ge 0}\\{3x + y \le 21}\\{x + y \le 9}\\{x + 4y \le 24}\end{array}\,\,\,} \right.} \right.\left( * \right)\)

Số điểm thưởng nhận được sẽ là P(x;y) = 60x + 80y.

Ta đi tìm giá trị nhỏ nhất của biểu thức P với x, y thỏa mãn (∗)

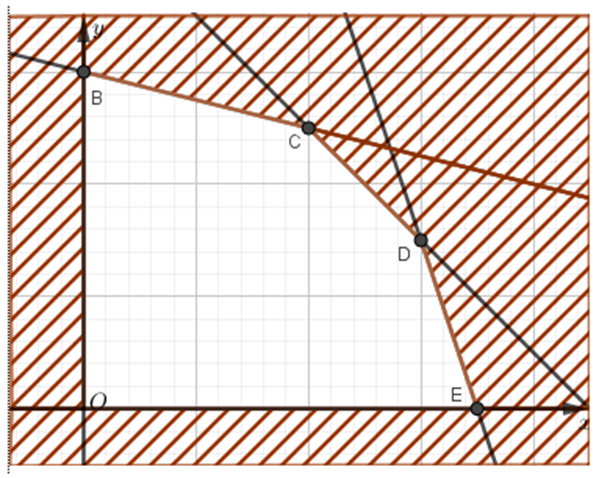
Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 24g hương liệu (ảnh 1)

Miền nghiệm là phần hình vẽ không tô màu ở hình trên, hay là ngũ giác OBCDE với O(0;0), B(0;6), C(4;5), D(6;3), E(7;0).

Biểu thức P = 60x + 80y đạt GTLN tại (x;y) là tọa độ một trong các đỉnh của ngũ giác.

Thay lần lượt tọa độ các điểm O, B, C, D, E vào biểu thức P(x;y) ta được:

P(0;0) = 0; P(0;6) = 480; P(4;5) = 640; P(6;3) = 600; P(7;0) = 420.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipid trong thức ăn mỗi ngày. Mỗi kilôgam thịt bò chứa 800 đơn vị protein và 200 đơn vị lipid. Mỗi kilôgam thịt lợn chứa 600 đơn vị protein và 400 đơn vị lipid. Biết rằng gia đình này chỉ mua nhiều nhất là 1,6kg thịt bò và 1,1kg thịt lợn; giá tiền 1kg thịt bò là 250 nghìn đồng; 1kg thịt lợn là 160 nghìn đồng. Giả sử gia đình đó mua x kilôgam thịt bò và y kilôgam thịt lợn.

a) Viết các bất phương trình biểu thị các điều kiện của bài toán thành một hệ bất phương trình rồi xác định miền nghiệm của hệ đó.

b) Gọi F (nghìn đồng) là số tiền phải trả cho x kilôgam thịt bò và y kilôgam thịt lợn. Hãy biểu diễn F theo x và y.

c) Tìm số kilôgam thịt mỗi loại mà gia đình cần mua để chi phí là ít nhất.

Xem đáp án

Lời giải

Số kilôgam thịt bò gia đình mua là x (kg); số kilôgam thịt lợn gia đình mua là y (kg). Vì số kilôgam thịt bò mua nhiều nhất là 1,6 kg và số kilôgam thịt lợn mua nhiều nhất là 1,1 kg nên ta có:

0 ≤ x ≤ 1,6; 0 ≤ y ≤ 1,1 (1)

Vì mỗi kilôgam thịt bò có chứa 800 đơn vị protein và mỗi kilôgam thịt lợn có chứa 600 đơn vị protein nên khối lượng protein có trong x kg thịt bò và y kg thịt lợn là: 800x + 600y (đơn vị).

Mà mỗi ngày gia đình cần ít nhất 900 đơn vị protein nên ta có bất phương trình:

800x + 600y ≥ 900 (2)

Vì mỗi kilôgam thịt bò có chứa 200 đơn vị lipid và mỗi kilôgam thịt lợn có chứa 400 đơn vị lipid nên khối lượng lipid có trong x kg thịt bò và y kg thịt lợn là: 200x + 400y (đơn vị).

Mà mỗi ngày gia đình cần ít nhất 400 đơn vị lipid nên ta có bất phương trình:

200x + 400y ≥ 400 (3)

Từ (1); (2); (3) ta có hệ bất phương trình:

\[\left\{ \begin{array}{l}0 \le x \le 1,6\\0 \le y \le 1,1\\800x + 600y \ge 900\\200x + 400y \ge 400\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}0 \le x \le 1,6\\0 \le y \le 1,1\\8x + 6y \ge 9\\x + 2y \ge 2\end{array} \right.\]

Ta đi xác định miền nghiệm của hệ bất phương trình.

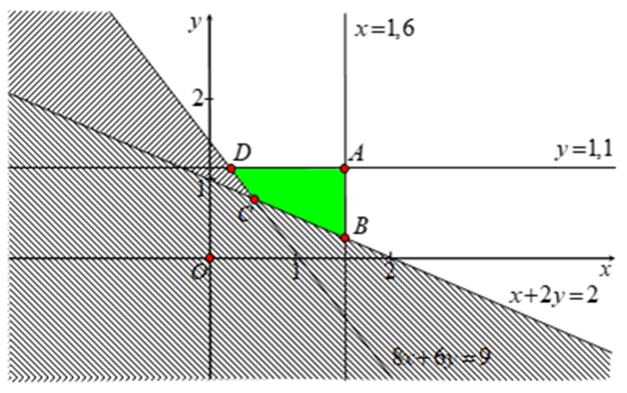
Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipid trong thức ăn mỗi (ảnh 1)

Miền nghiệm của hệ bất phương trình là tứ giác ABCD có trong hình vẽ trên với tọa độ các đỉnh là A(0,3; 1,1), B(0,6; 0,7), C(1,6; 0,2), D(1,6; 1,1).

b) Số tiền mua một kilôgam thịt bò là 250 nghìn đồng và số tiền mua một kilôgam thịt lợn là 160 nghìn đồng nên số tiền để mua x kg thịt bò và y kg thịt lợn là: F(x; y) = 250x + 160y (nghìn đồng).

c) Người ta đã chứng minh được để số tiền mua ít nhất thì (x; y) là tọa độ của một trong bốn đỉnh tứ giác ABCD.

Ta có: F(x; y) = 250x + 160y. Khi đó:

F(0,3; 1,1) = 250 . 0,3 + 160 . 1,1 = 251;

F(0,6; 0,7) = 250 . 0,6 + 160 . 0,7 = 262;

F(1,6; 0,2) = 250 . 1,6 + 160 . 0,2 = 432;

F(1,6; 1,1) = 250 . 1,6 + 160 . 1,1 = 576;

Suy ra giá trị nhỏ nhất cần tìm là F(0,3; 1,1) = 251.

Vậy để chi phí là ít nhất thì gia đình cần mua 0,3 kilôgam thịt bò và 1,1 kilôgam thịt lợn.

Câu 2

Cho hai tập khác rỗng A = (m ‒ 1; 4) ]; B = (‒2; 2m + 2) ,m ∈ ℝ. Tìm m để A ∩ B ≠ ∅.

A. ‒2 < m < 5.

B. m > ‒3.

C. ‒1< m < 5.

D. 1 < m < 5.

Lời giải

Đáp án đúng là: A

Do A, B ≠ ∅ ta có điều kiện \(\left\{ {\begin{array}{*{20}{l}}{m - 1 < 4}\\{2m + 2 > - 2}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m < 5}\\{m > - 2}\end{array} \Leftrightarrow - 2 < m < 5} \right.} \right.\)

Để A ∩ B = ∅ ⇔ 2m + 2 ≤ m ‒ 1 ⇔ m ≤ ‒3 (không thỏa điều kiện ‒2 < m < 5 )

Do đó không có giá trị nào của m để A, B ≠ ∅.

Vậy với mọi m ∈ (‒2; 5) thì A ∩B ≠ ∅.

Đáp án B sai vì học sinh không tìm điều kiện.

Đáp án C sai vì học sinh giải sai m ‒ 1 > ‒2 ⇔ m > ‒1 và kết hợp với điều kiện.

Đáp án D sai vì học sinh giải sai 4 < 2m + 2 ⇔ m > 1. Kết hợp với điều kiện.

Đáp án cần chọn là: A

Câu 3