Cho hình lăng trụ ABC.A'B'C có đáy là tam giác đều cạnh a. Mặt bên BB'C'C' là hình thoi và nằm trong mặt phẳng vuông góc với đáy. Khoảng cách giữa CC' và mặt phẳng (ABB'A) bằng \[\frac{{a\sqrt {12} }}{5}.\] Thể tích khối lăng trụ ABC.A'B'C bằng:
Cho hình lăng trụ ABC.A'B'C có đáy là tam giác đều cạnh a. Mặt bên BB'C'C' là hình thoi và nằm trong mặt phẳng vuông góc với đáy. Khoảng cách giữa CC' và mặt phẳng (ABB'A) bằng \[\frac{{a\sqrt {12} }}{5}.\] Thể tích khối lăng trụ ABC.A'B'C bằng:
A. \(\frac{{{a^3}}}{6}.\)
B. \(\frac{{{a^3}\sqrt {21} }}{{14}}.\)
C. \(\frac{{3{a^3}}}{8}.\)
D. \(\frac{{{a^3}\sqrt {21} }}{7}.\)
Quảng cáo
Trả lời:
Đáp án đúng là: B
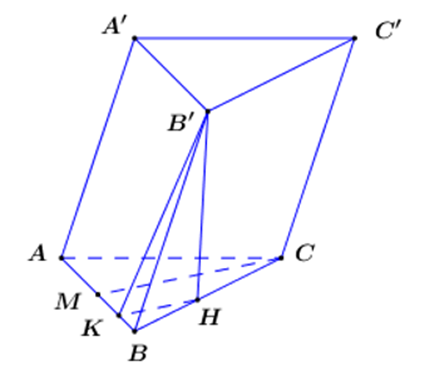
Kẻ B’H ⊥ Bc (H ∈ BC).
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{\left( {BCC'B'} \right) \bot \left( {ABC} \right) = BC}\\{B'H \subset \left( {BCC'B'} \right);B'H \bot BC}\end{array} \Rightarrow B'H \bot \left( {ABC} \right)} \right.\).
Đặt \(B'H = x(x > 0)\)
\( \Rightarrow BH = \sqrt {{a^2} - {x^2}} \) (Định lí Pytago trong tam giác vuông BB’H ).
Gọi M là trung điềm của AB ta có CM ⊥ AB và \(CM = \frac{{a\sqrt 3 }}{2}\) (do ∆ABC đều ạnh \({\rm{a}}\) ).
Trong (ABC) kẻ HK // CM (K ∈ AB), áp dụng định lí Ta−lét ta có:
\(\frac{{HK}}{{CM}} = \frac{{BH}}{{BC}} \Rightarrow \frac{{HK}}{{\frac{{a\sqrt 3 }}{2}}} = \frac{{\sqrt {{a^2} - {x^2}} }}{a} \Rightarrow HK = \frac{{\sqrt 3 \sqrt {{a^2} - {x^2}} }}{2}.\)
Áp dụng định lí Pytago trong tam giác vuông B’HK ta có:
\(B'{K^2} = B'{H^2} + H{K^2} = {x^2} + \frac{3}{4}\left( {{a^2} - {x^2}} \right) = \frac{3}{4}{a^2} + \frac{1}{4}{x^2} \Rightarrow B'K = \frac{{\sqrt {3{a^2} + {x^2}} }}{2}\)
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{AB \bot B'H}\\{AB \bot HK\left( {HK\,{\rm{//}}\,CM} \right)}\end{array} \Rightarrow AB \bot \left( {B'HK} \right) \Rightarrow AB \bot B'K} \right.\).
Khi đó ta có: \({S_{ABB'A'}} = B'K.AB = \frac{{a\sqrt {3{a^2} + {x^2}} }}{2}\)
Ta có: \(CC'\,{\rm{//}}\,BB' \Rightarrow CC'\,{\rm{//}}\,\left( {ABB'A'} \right)\)
\( \Rightarrow d\left( {CC';\left( {ABB'A'} \right)} \right) = d\left( {C;\left( {ABB'A'} \right)} \right) = \frac{{a\sqrt {12} }}{5}\).
\( \Rightarrow {V_{C \cdot ABB'A'}} = \frac{1}{3}{S_{ABB'A'}} \cdot d\left( {C;\left( {ABB'A'} \right)} \right)\)
\( = \frac{1}{3} \cdot \frac{{a\sqrt {3{a^2} + {x^2}} }}{2} \cdot \frac{{a\sqrt {12} }}{5}\)
\( = \frac{{{a^2}\sqrt {12} \sqrt {3{a^2} + {x^2}} }}{{30}} = \frac{2}{3}{V_{ABC \cdot A'B'C'}}\)
\( \Rightarrow {V_{ABC \cdot A'B'C'}} = \frac{3}{2} \cdot \frac{{{a^2}\sqrt {12} \sqrt {3{a^2} + {x^2}} }}{{30}} = \frac{{{a^2}\sqrt {12} \sqrt {3{a^2} + {x^2}} }}{{20}}\)
Lại có: \({V_{ABC \cdot A'B'C'}} = B'H \cdot {S_{\Delta ABC}} = x \cdot \frac{{{a^2}\sqrt 3 }}{4}\)
\( \Rightarrow \frac{{{a^2}\sqrt {12} \sqrt {3{a^2} + {x^2}} }}{{20}} = x \cdot \frac{{{a^2}\sqrt 3 }}{4}\)
\( \Leftrightarrow \frac{{2\sqrt {3{a^2} + {x^2}} }}{5} = x \Leftrightarrow 4\left( {3{a^2} + {x^2}} \right) = 25{x^2}\)
\( \Leftrightarrow 21{x^2} = 12{a^2} \Leftrightarrow x = \frac{{2\sqrt 7 }}{7}a\)
Vậy \({V_{ABC \cdot A'B'C'}} = x \cdot \frac{{{a^2}\sqrt 3 }}{4} = \frac{{2\sqrt 7 }}{7} \cdot \frac{{{a^2}\sqrt 3 }}{4} = \frac{{\sqrt {21} {a^3}}}{{14}}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Số kilôgam thịt bò gia đình mua là x (kg); số kilôgam thịt lợn gia đình mua là y (kg). Vì số kilôgam thịt bò mua nhiều nhất là 1,6 kg và số kilôgam thịt lợn mua nhiều nhất là 1,1 kg nên ta có:
0 ≤ x ≤ 1,6; 0 ≤ y ≤ 1,1 (1)
Vì mỗi kilôgam thịt bò có chứa 800 đơn vị protein và mỗi kilôgam thịt lợn có chứa 600 đơn vị protein nên khối lượng protein có trong x kg thịt bò và y kg thịt lợn là: 800x + 600y (đơn vị).
Mà mỗi ngày gia đình cần ít nhất 900 đơn vị protein nên ta có bất phương trình:
800x + 600y ≥ 900 (2)
Vì mỗi kilôgam thịt bò có chứa 200 đơn vị lipid và mỗi kilôgam thịt lợn có chứa 400 đơn vị lipid nên khối lượng lipid có trong x kg thịt bò và y kg thịt lợn là: 200x + 400y (đơn vị).
Mà mỗi ngày gia đình cần ít nhất 400 đơn vị lipid nên ta có bất phương trình:
200x + 400y ≥ 400 (3)
Từ (1); (2); (3) ta có hệ bất phương trình:
\[\left\{ \begin{array}{l}0 \le x \le 1,6\\0 \le y \le 1,1\\800x + 600y \ge 900\\200x + 400y \ge 400\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}0 \le x \le 1,6\\0 \le y \le 1,1\\8x + 6y \ge 9\\x + 2y \ge 2\end{array} \right.\]
Ta đi xác định miền nghiệm của hệ bất phương trình.
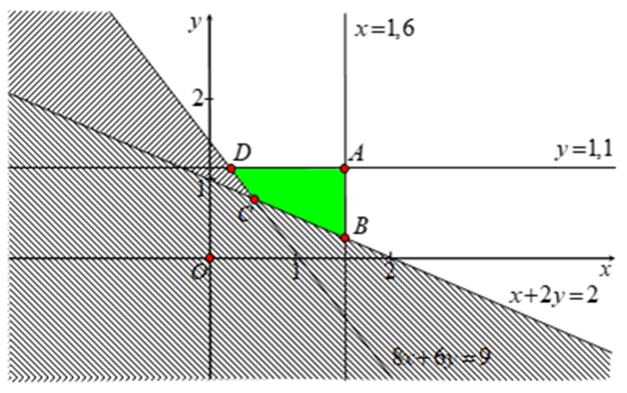
Miền nghiệm của hệ bất phương trình là tứ giác ABCD có trong hình vẽ trên với tọa độ các đỉnh là A(0,3; 1,1), B(0,6; 0,7), C(1,6; 0,2), D(1,6; 1,1).
b) Số tiền mua một kilôgam thịt bò là 250 nghìn đồng và số tiền mua một kilôgam thịt lợn là 160 nghìn đồng nên số tiền để mua x kg thịt bò và y kg thịt lợn là: F(x; y) = 250x + 160y (nghìn đồng).
c) Người ta đã chứng minh được để số tiền mua ít nhất thì (x; y) là tọa độ của một trong bốn đỉnh tứ giác ABCD.
Ta có: F(x; y) = 250x + 160y. Khi đó:
F(0,3; 1,1) = 250 . 0,3 + 160 . 1,1 = 251;
F(0,6; 0,7) = 250 . 0,6 + 160 . 0,7 = 262;
F(1,6; 0,2) = 250 . 1,6 + 160 . 0,2 = 432;
F(1,6; 1,1) = 250 . 1,6 + 160 . 1,1 = 576;
Suy ra giá trị nhỏ nhất cần tìm là F(0,3; 1,1) = 251.
Vậy để chi phí là ít nhất thì gia đình cần mua 0,3 kilôgam thịt bò và 1,1 kilôgam thịt lợn.
Câu 2
A. ‒2 < m < 5.
B. m > ‒3.
C. ‒1< m < 5.
D. 1 < m < 5.
Lời giải
Đáp án đúng là: A
Do A, B ≠ ∅ ta có điều kiện \(\left\{ {\begin{array}{*{20}{l}}{m - 1 < 4}\\{2m + 2 > - 2}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m < 5}\\{m > - 2}\end{array} \Leftrightarrow - 2 < m < 5} \right.} \right.\)
Để A ∩ B = ∅ ⇔ 2m + 2 ≤ m ‒ 1 ⇔ m ≤ ‒3 (không thỏa điều kiện ‒2 < m < 5 )
Do đó không có giá trị nào của m để A, B ≠ ∅.
Vậy với mọi m ∈ (‒2; 5) thì A ∩B ≠ ∅.
Đáp án B sai vì học sinh không tìm điều kiện.
Đáp án C sai vì học sinh giải sai m ‒ 1 > ‒2 ⇔ m > ‒1 và kết hợp với điều kiện.
Đáp án D sai vì học sinh giải sai 4 < 2m + 2 ⇔ m > 1. Kết hợp với điều kiện.
Đáp án cần chọn là: A
Câu 3
A. \[ - \frac{1}{{{x^3}}}.\]
B. \[ - \frac{1}{x}.\]
C. \[ - \frac{2}{{{x^3}}}.\]
D. \[ - \frac{1}{{{x^4}}}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. Luôn chọn A.
B. Luôn chọn B.
C. Giếng 20m chọn A còn giếng 25m chọn B.
D. Giếng 20 m chọn B còn giếng 25 m chọn A.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. {3; 4}.
B. {1; 2; 3; 4}.
C. {1; 2}.
D. ∅.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.