Cho hàm số y = ax3 + bx2 + cx + d (a, b, c, d ∈ ℝ) có đồ thị là đường cong trong hình bên. Có bao nhiêu số dương trong các số a, b, c, d?
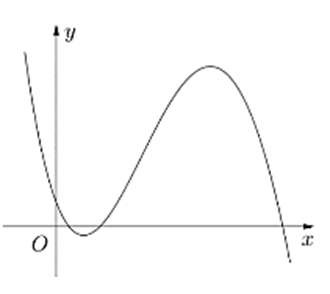
Cho hàm số y = ax3 + bx2 + cx + d (a, b, c, d ∈ ℝ) có đồ thị là đường cong trong hình bên. Có bao nhiêu số dương trong các số a, b, c, d?

Quảng cáo
Trả lời:
Từ đồ thị ta có: \[\mathop {\lim }\limits_{x \to + \infty } y = - \infty \Rightarrow a < 0\]
Gọi x1 và x2 lần lượt là hai điểm cực trị của hàm số đã cho (x1 < x2)
Từ đồ thị ta thấy: x1 + x2 > 0
Þ ab < 0 Þ b > 0
Lại có: x1.x2 > 0 Þ ac > 0 Þ c > 0
Đồ thị hàm số giao với trục tung tại điểm có tung độ y
Þ d > 0
Vậy trong các số a, b, c, d có 2 số dương.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Để \[A \cap B \ne \emptyset \] thì \[\left\{ \begin{array}{l}m + 1 \le 1\\m \ge 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \le 0\\m \ge 4\end{array} \right.\]
Vậy để \[A \cap B \ne \emptyset \] thì m Î (0; 4).
Lời giải
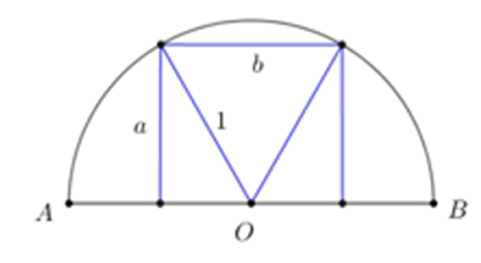
Gọi kích thước của miếng tôn như hình vẽ.
Áp dụng định lý Py-ta-go ta có:
\[{a^2} + {\left( {\frac{b}{2}} \right)^2} = 1 \Leftrightarrow {a^2} = \frac{{4 - {b^2}}}{4} \Leftrightarrow a = \frac{{\sqrt {4 - {b^2}} }}{2}\]
Khi đó diện tích miếng tôn hình chữ nhật là:
\[S = ab = \frac{{b\sqrt {4 - {b^2}} }}{2}\]
Áp dụng bất đẳng thức Cô-si cho hai số ta có:
\[{b^2} + \sqrt {{{\left( {4 - {b^2}} \right)}^2}} \ge 2b\sqrt {4 - {b^2}} \]
\[ \Leftrightarrow b\sqrt {4 - {b^2}} \le \frac{{{b^2} + 4 - {b^2}}}{2} = 2\]
\[ \Rightarrow S = \frac{{b\sqrt {4 - {b^2}} }}{2} \le 1\]
Dấu “=” xảy ra \[b = \sqrt {4 - {b^2}} \Leftrightarrow {b^2} = 4 - {b^2} \Leftrightarrow b = \sqrt 2 \]
Vậy diện tích lớn nhất có thể là 1m2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
11- Hà Thị Bích Ngọc
Sao b c d đều lớn hơn 0 lại chỉ có 2 số dương vậy
Xem tất cả 1 phản hồi
Kim Danh
chỉ có b,d>0 ; ac>0 mà a<0 => c<0