Cho đường tròn (O) bán kính OA. Từ trung điểm M của OA vẽ dây BC vuông góc với OA. Biết độ dài đường tròn (O) là 4π (cm). Độ dài cung lớn BC là:
Cho đường tròn (O) bán kính OA. Từ trung điểm M của OA vẽ dây BC vuông góc với OA. Biết độ dài đường tròn (O) là 4π (cm). Độ dài cung lớn BC là:
A. \(\frac{{4\pi }}{3}\)
B. \(\frac{{5\pi }}{3}\)
C. \(\frac{{7\pi }}{3}\)
D. \(\frac{{8\pi }}{3}\).
Quảng cáo
Trả lời:
Đáp án đúng là: D
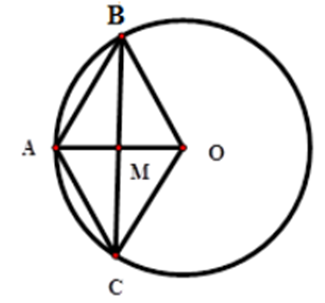
Vì độ dài đường tròn là 4π nên 4π = 2π . R
Suy ra R = 2 (cm)
Xét tứ giác ABOC có hai đường chéo AO và BC vuông góc với nhau tại trung điểm M nên ABOC là hình thoi
Suy ra OB = OC = AB
Do đó tam giác ABO đều nên \(\widehat {AOB} = 60^\circ \)
Suy ra \(\widehat {BOC} = 2\widehat {AOB} = 2.60^\circ = 120^\circ \)
Do đó số đo cung lớn BC là 360° – 120° = 240°
Độ dài cung lớn BC là \(l = \frac{{\pi .2.240^\circ }}{{180^\circ }} = \frac{{8\pi }}{3}\) (cm)
Vậy ta chọn đáp án D.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. 500 đơn vị vitamin A và 500 đơn vị vitamin B.
B. 600 đơn vị vitamin A và 400 đơn vị vitamin B.
C. 600 đơn vị vitamin A và 300 đơn vị vitamin B.
D. 100 đơn vị vitamin A và 300 đơn vị vitamin B.
Lời giải
Đáp án đúng là: D
Gọi x là số đơn vị vitamin A mỗi người tiếp nhận trong một ngày (x ≥ 0).
Gọi y là số đơn vị vitamin A mỗi người tiếp nhận trong một ngày (y ≥ 0).
Một người có thể tiếp nhận được mỗi ngày không quá 600 đơn vị vitamin A và không quá 500 đơn vị vitamin B nên x ≤ 600 và y ≤ 500.
Một người mỗi ngày cần từ 400 đến 1 000 đơn vị vitamin cả A và B nên:
400 ≤ x + y ≤ 1000
Do tác động phối hợp của hai loại vitamin, mỗi ngày, số đơn vị vitamin B không ít hơn \(\frac{1}{2}\) số đơn vị vitamin A nhưng không nhiều hơn ba lần số đơn vị vitamin A nên:
\(\left\{ \begin{array}{l}y \ge \frac{1}{2}x\\y \le 3{\rm{x}}\end{array} \right.\)
Ta có hệ bất phương trình giữa x và y: \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x \le 600\\y \le 500\\x + y \ge 400\\x + y \le 1000\\y \ge \frac{1}{2}x\\y \le 3{\rm{x}}\end{array} \right.\)
Biểu diễn miền nghiệm của hệ bất phương trình:
− Biểu diễn miền nghiệm D1 của bất phương trình x ≤ 600
+ Vẽ đường thẳng d1: x = 600 trên mặt phẳng tọa độ Oxy
+ Thay x = 0, y = 0 vào bất phương trình ta được 0 ≤ 600 là mệnh đề đúng nên tọa độ điểm O(0; 0) thỏa mãn bất phương trình x ≤ 600
Vậy miền nghiệm D1 của bất phương trình x ≤ 600 là nửa mặt phẳng bờ d1 (kể cả bờ d1) chứa điểm O.
Tương tự ta biểu diễn các miền nghiệm:
− Miền nghiệm D2 của bất phương trình y ≤ 500: là nửa mặt phẳng bờ d2 (kể cả bờ d2: y = 500) chứa điểm O.
− Miền nghiệm D3 của bất phương trình x + y ≥ 400: là nửa mặt phẳng bờ d3 (kể cả bờ d3: x + y = 400) không chứa điểm O.
− Miền nghiệm D4 của bất phương trình x + y ≤ 1000: là nửa mặt phẳng bờ d4 (kể cả bờ d4: x + y = 1000) chứa điểm O.
− Miền nghiệm D5 của bất phương trình \(y \ge \frac{1}{2}x\): là nửa mặt phẳng bờ d5 (kể cả bờ d5: \(y = \frac{1}{2}x\) ) chứa điểm M(0; 50).
− Miền nghiệm D6 của bất phương trình y ≤ 3x: là nửa mặt phẳng bờ d6 (kể cả bờ d6: y = 3x) không chứa điểm M (0; 50).
Ta có đồ thị sau:
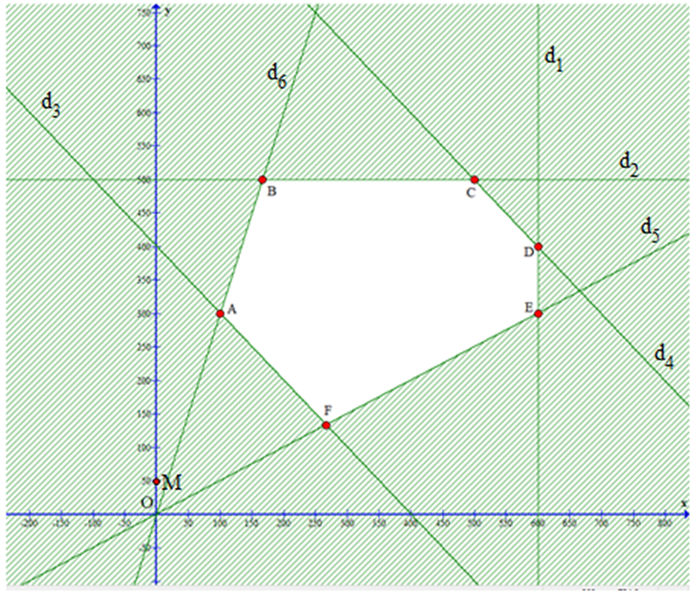
Miền nghiệm của hệ bất phương trình là miền của đa giác ABCDEF với: \(A\left( {100;300} \right),B\left( {\frac{{500}}{3};500} \right),C\left( {500;500} \right),D\left( {600;400} \right),E\left( {600;300} \right);F\left( {\frac{{800}}{3};\frac{{400}}{3}} \right)\)
Số tiền trả cho x đơn vị vitamin A và y đơn vị vitamin B là: F(x; y) = 9x + 7,5y
Để có số tiền phải trả là ít nhất thì F(x; y) phải nhỏ nhất
Tại A(100; 300): F = 9.100 + 7,5. 300 = 3150;
Tại \(B\left( {\frac{{500}}{3};500} \right):F = 9.\frac{{500}}{3} + 7,5.500 = 5250\)
Tại C(500; 500): F = 9. 500 + 7,5. 500 = 8250;
Tại D(600, 400): F = 9. 600 + 7,5. 400 = 8400;
Tại E(600, 300): F = 9. 600 + 7,5. 300 = 7650;
Tại \(F\left( {\frac{{800}}{3};\frac{{400}}{3}} \right):F = 9.\frac{{800}}{3} + 7,5.\frac{{400}}{3} = 3400\).
Suy ra F(x; y) nhỏ nhất là 3150 khi x = 100 và y = 300
Do đó mỗi người sẽ dùng 100 đơn vị vitamin A và 300 đơn vị vitamin B để đảm bảo các điều kiện số lượng sử dụng và chi phí phải trả là ít nhất
Vậy ta chọn đáp án D.
Lời giải
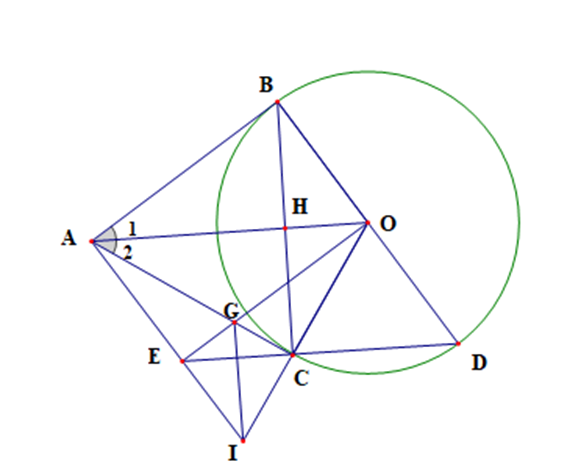
a) Xét (O) có AB, AC là hai tiếp tuyến cắt nhau tại A nên AB = AC và AO là tia phân giác của \(\widehat {BAC}\)
Do đó ∆ABC cân tại A có AO là phân giác đồng thời là đường cao, hay AO ⊥ BC.
b) Vì ∆BCD nội tiếp đường tròn (O) nên ∆BCD vuông tại C
Do đó CD ⊥ BC
Mà AO ⊥ BC nên CD // AO.
c) Vì ∆AOB vuông tại B nên theo định lý Pythagore có:
\[AB = \sqrt {A{O^2} - B{O^2}} = \sqrt {{5^2} - {3^2}} = 4\]
Gọi H là giao điểm của AO và BC.
Áp dụng hệ thức lượng trong tam giác vuông ABO có:
⦁ AB2 = AH . AO \( \Rightarrow AH = \frac{{A{B^2}}}{{AO}} = \frac{{16}}{5} = 3,2\)
⦁ \(\frac{1}{{B{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{B{O^2}}} \Leftrightarrow \frac{1}{{B{H^2}}} = \frac{1}{{{4^2}}} + \frac{1}{{{3^2}}}\). Suy ra BH = 2,4
Do đó BC = 2AH = 2 . 2,4 = 4,8
Chu vi tam giác ABC là: AB + AC + BC = 4 + 4 + 4,8 = 12,8 (cm).
Diện tích tam giác ABC là \({S_{ABC}} = \frac{1}{2}AH.BC = \frac{1}{2}.3,2.4,8 = 7,68\) (cm2).
d) Vì AO // CD nên \(\widehat {BOA} = \widehat {O{\rm{D}}E}\) (hai góc đồng vị)
Xét ∆ABO và ∆EOD có
\(\widehat {ABO} = \widehat {EO{\rm{D}}}\left( { = 90^\circ } \right)\);
BO = DO;
\(\widehat {BOA} = \widehat {O{\rm{D}}E}\) (chứng minh trên)
Suy ra ∆ABO = ∆EOD (g.c.g)
Do đó AB = EO (hai cạnh tương ứng)
Mà AB // EO (vì cùng vuông góc với BD)
Nên ABOE là hình bình hành
Lại có \(\widehat {AOB} = 90^\circ \) nên hình bình hành ABOE là hình chữ nhật.
Suy ra \(\widehat {A{\rm{E}}O} = 90^\circ \) hay OE ⊥ AI
Xét tam giác AIO có hai đường cao OE và AC cắt nhau tại G
Suy ra G là trực tâm, nên OA ⊥ GI
Xét (O) có AB, AC là hai tiếp tuyến cắt nhau tại A nên OA là tia phân giác của \(\widehat {BOC}\)
Do đó \(\widehat {I{\rm{O}}A} = \widehat {BOA}\)
Mà \(\widehat {O{\rm{D}}E} = \widehat {BOA}\) suy ra \(\widehat {I{\rm{O}}A} = \widehat {ODE}\) (1)
Ta có EO ⊥ AI, EO ⊥ OD suy ra AE // OD
Mà AO // ED nên AODE là hình bình hành
Suy ra \(\widehat {O{\rm{D}}E} = \widehat {OA{\rm{E}}}\) (2)
Từ (1) và (2) suy ra \(\widehat {I{\rm{O}}A} = \widehat {OAE}\)
Do đó tam giác AOI cân tại I
Lại có IG là đường cao
Suy ra IG là đường trung trực của AO
Vậy IG là đường trung trực của AO.
Câu 3
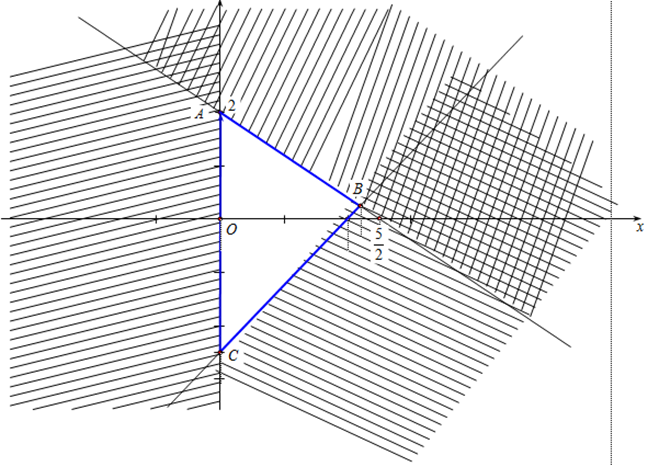
A. \(\left\{ \begin{array}{l}y \ge 0\\5{\rm{x}} - 4y \ge 10\\5{\rm{x}} + 4y \le 10\end{array} \right.\)
B. \(\left\{ \begin{array}{l}x \ge 0\\{\rm{4x}} - 5y \le 10\\5{\rm{x}} + 4y \le 10\end{array} \right.\)
C. \(\left\{ \begin{array}{l}x \ge 0\\5{\rm{x}} - 4y \le 10\\{\rm{4x}} + 5y \le 10\end{array} \right.\)
D. \(\left\{ \begin{array}{l}x > 0\\5{\rm{x}} - 4y \le 10\\{\rm{4x}} + 5y \le 10\end{array} \right.\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.