Tính tổng các nghiệm nguyên của bất phương trình: log2 (x2 + 3) − log2 x + x2 − 4x + 1 ≤ 0

Câu hỏi:

11/07/2024 8,607

Tính tổng các nghiệm nguyên của bất phương trình:

log₂ (x² + 3) − log₂ x + x² − 4x + 1 ≤ 0

Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!

Sách mới 2k7: Bộ 20 đề minh họa Toán, Lí, Hóa, Văn, Sử, Địa…. form chuẩn 2025 của Bộ giáo dục (chỉ từ 49k/cuốn).

Đề toán-lý-hóa Đề văn-sử-địa Tiếng anh & các môn khác

Quảng cáo

Trả lời:

Giải bởi Vietjack

ĐK: x > 0

log₂ (x² + 3) − log₂ x + x² − 4x + 1 ≤ 0

Û log₂ (x² + 3) + (x² + 3) ≤ log₂ 4x + 4x (*)

Xét hàm số f (t) = t + log₂ t trên khoảng (0; +∞) có:

\(f'\left( t \right) = 1 + \frac{1}{{t\ln 2}} > 0,\;\forall t \in \left( {0;\; + \infty } \right)\)

Ta thấy hàm số y = f (t) luôn đồng biến trên (0; +∞)

Do đó bất phương trình (*) tương đương: x² + 3 ≤ 4x

Û x² − 4x + 3 ≤ 0

Û −1 ≤ x ≤ 3

Kết hợp điều kiện suy ra tập nghiệm nguyên của bất phương trình là S = {1; 2; 3}

Vậy S = 1 + 2 + 3 = 6.

Nhà sách VIETJACK:

Xem thêm kho sách »

Combo - Sổ tay kiên thức trọng tâm Toán, Lí, Hóa dành cho 2k7 VietJack

₫29.000 (Đã bán 152)

Sách - Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 cho 2k7 VietJack

₫140.000 ₫300.000 (Đã bán 1,2k)

Sách Combo - Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) - 2025 cho 2k7 VietJack

₫140.000 ₫300.000 (Đã bán 1,6k)

Sách - Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 cho 2k7 VietJack

₫140.000 ₫300.000 (Đã bán 2,7k)

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Tìm nguyên hàm của hàm số f (x) = cos² (2x).

Xem đáp án » 11/07/2024 25,873

Câu 2:

Có bao nhiêu cách xếp 6 cặp vợ chồng ngồi xung quanh một chiếc bàn tròn, sao cho mỗi bà đều ngồi cạnh chồng của mình?

Xem đáp án » 11/07/2024 21,468

Câu 3:

Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây?

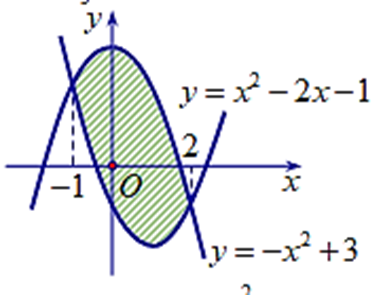
A. \(\int\limits_{ - 1}^2 {\left( {2{x^2} - 2x - 4} \right)dx} \);

B. \(\int\limits_{ - 1}^2 {\left( { - 2x + 2} \right)dx} \);

C. \(\int\limits_{ - 1}^2 {\left( {2x - 2} \right)dx} \);

D. \(\int\limits_{ - 1}^2 {\left( { - 2{x^2} + 2x + 4} \right)dx} \).

Xem đáp án » 26/09/2023 14,055

Câu 4:

Cho đa giác đều 2018 đỉnh. Hỏi có bao nhiêu tam giác có đỉnh là đỉnh của đa giác và có một góc lớn hơn 100°?

Xem đáp án » 11/07/2024 10,421

Câu 5:

Miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}2x + 3y - 6 < 0\\x \ge 0\\2x - 3y - 1 \le 0\end{array} \right.\) chứa điểm nào sau đây?

A. A(1; 2);

B. B(0; 2);

C. C(−1; 3);

D. \(D\left( {0;\; - \frac{1}{3}} \right)\).

Xem đáp án » 26/09/2023 9,058

Câu 6:

Trên mặt phẳng tọa độ Oxy, cho tam giác ABC biết A(1; 3), B(−2; −2), C(3; 1). Tính cosin góc A của tam giác.

Xem đáp án » 11/07/2024 6,676

Xem thêm các câu hỏi khác »

Tính tổng các nghiệm nguyên của bất phương trình:

log₂ (x² + 3) − log₂ x + x² − 4x + 1 ≤ 0

Nhà sách VIETJACK:

Bình luận

Tìm nguyên hàm của hàm số f (x) = cos² (2x).

Có bao nhiêu cách xếp 6 cặp vợ chồng ngồi xung quanh một chiếc bàn tròn, sao cho mỗi bà đều ngồi cạnh chồng của mình?

Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây?

Cho đa giác đều 2018 đỉnh. Hỏi có bao nhiêu tam giác có đỉnh là đỉnh của đa giác và có một góc lớn hơn 100°?

Miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}2x + 3y - 6 < 0\\x \ge 0\\2x - 3y - 1 \le 0\end{array} \right.\) chứa điểm nào sau đây?

Trên mặt phẳng tọa độ Oxy, cho tam giác ABC biết A(1; 3), B(−2; −2), C(3; 1). Tính cosin góc A của tam giác.

VIP +3 tháng ( 199,000 VNĐ )

VIP +6 tháng ( 299,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

Tính tổng các nghiệm nguyên của bất phương trình: log2 (x2 + 3) − log2 x + x2 − 4x + 1 ≤ 0

Nhà sách VIETJACK:

Bình luận

Tìm nguyên hàm của hàm số f (x) = cos2 (2x).

Có bao nhiêu cách xếp 6 cặp vợ chồng ngồi xung quanh một chiếc bàn tròn, sao cho mỗi bà đều ngồi cạnh chồng của mình?

Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây?

Cho đa giác đều 2018 đỉnh. Hỏi có bao nhiêu tam giác có đỉnh là đỉnh của đa giác và có một góc lớn hơn 100°?

Miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}2x + 3y - 6 < 0\\x \ge 0\\2x - 3y - 1 \le 0\end{array} \right.\) chứa điểm nào sau đây?

Trên mặt phẳng tọa độ Oxy, cho tam giác ABC biết A(1; 3), B(−2; −2), C(3; 1). Tính cosin góc A của tam giác.

VIP +3 tháng ( 199,000 VNĐ )

VIP +6 tháng ( 299,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Tính tổng các nghiệm nguyên của bất phương trình:

log₂ (x² + 3) − log₂ x + x² − 4x + 1 ≤ 0

Tìm nguyên hàm của hàm số f (x) = cos² (2x).