Rút gọn tổng sau: \(S = C_n^1 + 2C_n^2 + 3C_n^3 + ... + nC_n^n\) ta được:
Rút gọn tổng sau: \(S = C_n^1 + 2C_n^2 + 3C_n^3 + ... + nC_n^n\) ta được:
A. S = n . 2n
B. S = 2n+1
C. S = n. 2n-1
D. S = 2n-1.
Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: C
Ta có \(kC_n^k = k.\frac{{n!}}{{k!\left( {n - k} \right)!}} = \frac{{n\left( {n - 1} \right)!}}{{\left( {k - 1} \right)!\left[ {n - 1 - \left( {k - 1} \right)} \right]!}} = nC_{n - 1}^{k - 1}\)
Khi đó: \(S = C_n^1 + 2C_n^2 + 3C_n^3 + ... + nC_n^n\)
\(S = nC_{n - 1}^0 + nC_{n - 1}^1 + ... + nC_{n - 1}^{n - 1}\)
\(S = n\left( {C_{n - 1}^0 + C_{n - 1}^1 + ... + C_{n - 1}^{n - 1}} \right)\)
Ta có: \({\left( {a + b} \right)^{n - 1}} = C_{n - 1}^0.{a^{n - 1}} + C_{n - 1}^1.{a^{n - 2}}b + C_{n - 1}^2{a^{n - 3}}{b^2} + ... + C_{n - 1}^{n - 1}.{b^{n - 1}}\)
Thay a = 1,b = 1 vào biểu thức ta được
\({2^{n - 1}} = C_{n - 1}^0 + C_{n - 1}^1 + ... + C_{n - 1}^{n - 1}\)
Suy ra \(S = n\left( {C_{n - 1}^0 + C_{n - 1}^1 + ... + C_{n - 1}^{n - 1}} \right) = n{.2^{n - 1}}\)
Vậy ta chọn đáp án C.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) Vì nam nữ được sắp xếp tùy ý nên sử dụng hoán vị cho 5 nam + 5 nữ = 10 người
Suy ra có 10! = 3 628 800 cách xếp.
b) Chọn 1 dãy xếp nam ngồi có 2 cách.
Xếp 5 bạn nam vào các vị trí trong dãy đã chọn có 5! cách
Xếp nữ vào dãy còn lại có 1 cách
Xếp nữ vào các vị trí trong dãy đó có 5! cách
Suy ra có: 2 . 5! . 1 .5! = 28 800 cách.
Câu 2
A. \(\frac{{\sqrt {10} }}{4}\)
B. \(\frac{{\sqrt 6 }}{3}\)
C. \(\frac{{\sqrt 3 }}{3}\)
D. \(\frac{{\sqrt 6 }}{4}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là: D
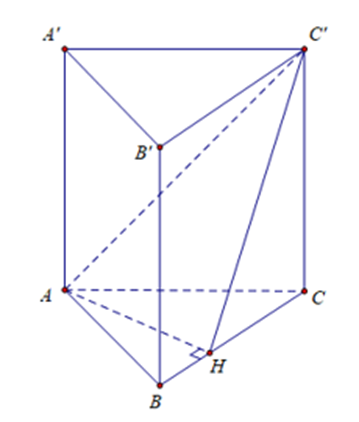
Gọi H là hình chiếu của A trên BC
Ta có AH ⊥ BC, AH ⊥ BB’ nên AH ⊥ (BCC’B’)
Suy ra HC’ là hình chiếu của AC’ trên mặt phẳng (BCC’B’)
Do đó góc giữa AC’ và mặt phẳng (BCC’B’) là góc \(\widehat {AC'H}\)
Vì tam giác ABC vuông tại A nên \[{{\rm{S}}_{ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}AH.BC\]
Vì tam giác ABC vuông tại A nên theo định lý Pytago có
\(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {3{{\rm{a}}^2} + {a^2}} = 2{\rm{a}}\)
Suy ra \(AH = \frac{{AC.AB}}{{BC}} = \frac{{a\sqrt 3 .a}}{{2{\rm{a}}}} = \frac{{a\sqrt 3 }}{2}\)
Vì tam giác AA’C’ vuông tại A’ nên theo định lý Pytago có
\(AC' = \sqrt {AA{'^2} + A'C{'^2}} = \sqrt {{{\rm{a}}^2} + {a^2}} = \sqrt 2 {\rm{a}}\)
Xét tam giác AC’H có
\[\sin \widehat {AC'H} = \frac{{AH}}{{AC'}} = \frac{{\frac{{a\sqrt 3 }}{2}}}{{a\sqrt 2 }} = \frac{{\sqrt 6 }}{4}\]
Vậy ta chọn đáp án D.
Câu 3
A. AM (M là trung điểm của AB)
B. AN (N là trung điểm của CD)
C. AH (H là hình chiếu của B trên CD)
D. AK (K là hình chiếu của C trên BD).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. 30°
B. 36°
C. 45°
D. 60°.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. Ω ={SS; NN; NS; SN}
B. Ω ={SS; NN; SN}
C. Ω ={SS; NN}
D. Ω ={SS; SN}.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. I(0; 0)
B. \(I\left( {\frac{{ - d}}{c};\frac{a}{c}} \right)\)
C. \(I\left( {\frac{a}{c};\frac{{ - d}}{c}} \right)\)
D. \(I\left( {\frac{d}{c};\frac{b}{a}} \right)\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập