Quảng cáo
Trả lời:
+ Xét hàm số y = –2x + 3
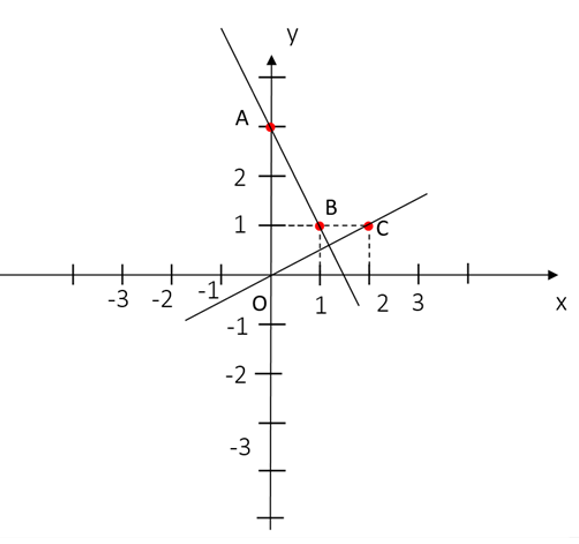
Cho x = 0 thì y = 3, ta được giao điểm của đồ thị hàm số y = –2x + 3 với trục Oy là A(0; 3).
Cho x = 1 thì y = 1, ta được điểm B(1; 1) thuộc đồ thị hàm số y = –2x + 3.
+ Xét hàm số y =
Cho x = 0 thì y = 0, ta được điểm ở gốc tọa độ O(0; 0) thuộc đồ thị hàm số y = .
Cho x = 2 thì y = 1, ta được điểm C(2; 1) thuộc đồ thị hàm số y = .
+ Đồ thị hàm số y = –2x + 3 là đường thẳng AB.
Đồ thị hàm số y = là đường thẳng OC.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Chi phí cố định hằng ngày là 36 triệu đồng nên b = 36, chi phí sản xuất mỗi chiếc xe đạp là 1,8 triệu đồng nên a = 1,8.
Do đó, công thức của hàm số bậc nhất biểu thị chi phí y (triệu đồng) để sản xuất x (xe đạp) trong một ngày là y = 1,8x + 36.
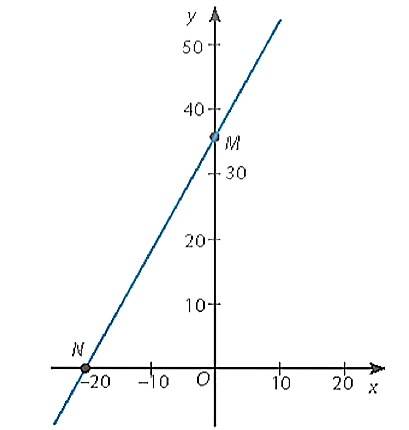
b) Cho x = 0 thì y = 36 ta được giao điểm của đồ thị hàm số với trục Oy là M(0; 36).
Cho y = 0 thì x = –20, ta được giao điểm của đồ thị hàm số với trục Ox là N(–20; 0).
Đồ thị của hàm số y = 1,8x + 36 là đường thẳng MN.
c) Chi phí để sản xuất 15 chiếc xe đạp (tức x = 15) trong 1 ngày là:
y = 1,8 . 15 + 36 = 63 (triệu đồng).
d) Thay y = 72 vào công thức hàm số y = 1,8x + 36 ta được:
72 = 1,8x + 36, suy ra x = 20 (chiếc xe).
Vậy với chi phí trong ngày là 72 triệu đồng thì có thể sản xuất được 20 chiếc xe đạp.
Lời giải
a) Công thức tính số điện cước điện thoại y (đồng) phải trả trong tháng khi gọi x phút là
y = 800x + 22 000 (đồng).
b) Số tiền cước điện thoại phải trả khi gọi 75 phút, tức là x = 75 là
y = 800 . 75 + 22 000 = 82 000 (đồng).
c) Nếu số tiền cước điện thoại phải trả là 94 000 đồng, tức y = 94 000, thay giá trị này vào công thức y = 800x + 22 000, ta được:
94 000 = 800x + 22 000, suy ra x = 90.
Vậy trong tháng đó thuê bao đã gọi 90 phút.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.