Câu hỏi:
12/07/2024 977
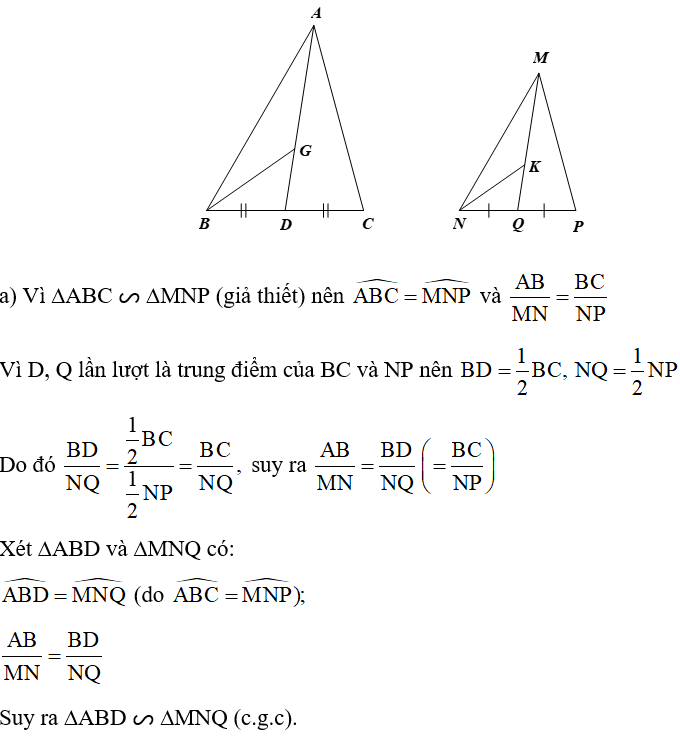
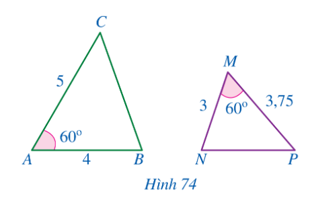
Đố. Chỉ sử dụng thước thẳng có chia đơn vị đến milimét và thước đo góc, làm thế nào đo được khoảng cách giữa hai vị trí B, C trên thực tế, biết rằng có vị trí A thoả mãn AB = 20 m, AC = 50 m,
Bạn Vy làm như sau: Vẽ tam giác A’B’C’ có A’B’ = 2 cm, A’C’ = 5 cm, Bạn Vy lấy thước đo khoảng cách giữa hai điểm B’, C’ và nhận được kết quả B’C’ ≈ 6,6 cm. Từ đó, bạn Vy kết luận khoảng cách giữa hai vị trí B, C trên thực tế khoảng 66 m. Em hãy giải thích tại sao bạn Vy có thể kết luận như vậy.
Đố. Chỉ sử dụng thước thẳng có chia đơn vị đến milimét và thước đo góc, làm thế nào đo được khoảng cách giữa hai vị trí B, C trên thực tế, biết rằng có vị trí A thoả mãn AB = 20 m, AC = 50 m,
Bạn Vy làm như sau: Vẽ tam giác A’B’C’ có A’B’ = 2 cm, A’C’ = 5 cm, Bạn Vy lấy thước đo khoảng cách giữa hai điểm B’, C’ và nhận được kết quả B’C’ ≈ 6,6 cm. Từ đó, bạn Vy kết luận khoảng cách giữa hai vị trí B, C trên thực tế khoảng 66 m. Em hãy giải thích tại sao bạn Vy có thể kết luận như vậy.
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho Hình 76, biết AB = 4, BC = 3, BE = 2, BD = 6. Chứng minh:
a) ∆ABD ᔕ ∆EBC;
b)
c) Tam giác DGE vuông.
Cho Hình 76, biết AB = 4, BC = 3, BE = 2, BD = 6. Chứng minh:
a) ∆ABD ᔕ ∆EBC;
b)
c) Tam giác DGE vuông.
Xem đáp án »
13/07/2024
3,005
Câu 2:
Cho ∆ABC ᔕ ∆MNP.
a) Gọi D và Q lần lượt là trung điểm của BC và NP. Chứng minh ∆ABD ᔕ ∆MNQ.
Cho ∆ABC ᔕ ∆MNP.
a) Gọi D và Q lần lượt là trung điểm của BC và NP. Chứng minh ∆ABD ᔕ ∆MNQ.
Xem đáp án »
13/07/2024
2,496
Câu 3:
Cho góc xOy. Trên tia Ox lấy các điểm A, B sao cho OA = 2 cm, OB = 9 cm. Trên tia Oy lấy các điểm M, N sao cho OM = 3 cm, ON = 6 cm. Chứng minh
Cho góc xOy. Trên tia Ox lấy các điểm A, B sao cho OA = 2 cm, OB = 9 cm. Trên tia Oy lấy các điểm M, N sao cho OM = 3 cm, ON = 6 cm. Chứng minh
Xem đáp án »
12/07/2024
2,035
Câu 4:
Cho Hình 74.
a) Chứng minh ∆ABC ᔕ ∆MNP.
b) Góc nào của tam giác ∆MNP bằng góc B?
c) Góc nào của tam giác ∆ABC bằng góc P?
Cho Hình 74.
a) Chứng minh ∆ABC ᔕ ∆MNP.
b) Góc nào của tam giác ∆MNP bằng góc B?
c) Góc nào của tam giác ∆ABC bằng góc P?
Xem đáp án »
13/07/2024
1,958
Câu 7:
Cho hai tam giác ABC và A’B’C’ lần lượt vuông tại A và A’ sao cho Chứng minh
Cho hai tam giác ABC và A’B’C’ lần lượt vuông tại A và A’ sao cho Chứng minh
Xem đáp án »
13/07/2024
1,452
về câu hỏi!