Câu hỏi:
13/07/2024 2,904
Để làm cây thông noel, người ta hàn một khung sắt có dạng hình tam giác cân ABC (AB = AC = 2 m) cùng các thanh sắt nằm ngang GF, HE, ID, BC và sau đó gắn cây thông như Hình 22. Tính số tiền sắt cần sử dụng để làm cây thông noel đó.
Biết giá một mét sắt là 55 000 đồng và AG = GH = HI = IB, CD = DE = EF = FA, thanh GF dài 0,2 m.
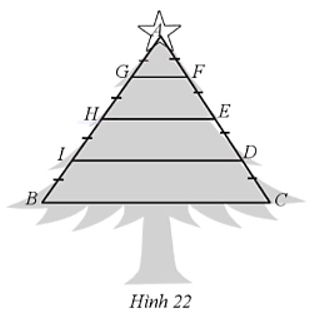
Để làm cây thông noel, người ta hàn một khung sắt có dạng hình tam giác cân ABC (AB = AC = 2 m) cùng các thanh sắt nằm ngang GF, HE, ID, BC và sau đó gắn cây thông như Hình 22. Tính số tiền sắt cần sử dụng để làm cây thông noel đó.
Biết giá một mét sắt là 55 000 đồng và AG = GH = HI = IB, CD = DE = EF = FA, thanh GF dài 0,2 m.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Do AG = GH nên G là trung điểm của AH.
AF = FE nên F là trung điểm AE.
Xét ∆AHE có G, F lần lượt là trung điểm của AH, AE nên GF là đường trung bình của ∆AHE
Nên HE = 2GF = 2.0,2 = 0,4 (m).
• Do AH = AG + GH, BH = BI + IH, mà AG = GH = BI = IH
Nên AH = BH, hay H là trung điểm của AB.
• Do AE = AF + FE, EC = ED + CD, mà AF = FE = ED = CD
Nên AE = EC, hay E là trung điểm của AC.
Xét ∆ABC có H, E lần lượt là trung điểm của AB, AC nên HE là đường trung bình của ∆ABC, do đó BC = 2HE = 2.0,4 = 0,8 (m).
Ta có AI = 3BI, AB = 4BI nên
AD = 3CD, AC = 4CD nên
Do đó,
Xét ∆ABC có theo định lí Thalès đảo ta có ID // BC.
Theo hệ quả của định lí Thalès, ta có
Suy ra (m).
Số mét sắt cần sử dụng để làm cây thông noel đó là:
GF + HE + ID + BC + AB + AC = 0,2 + 0,4 + 0,6 + 0,8 + 2 + 2 = 6 (m).
Vậy số tiền cần trả để hoàn thành cây thông noel đó là:
6.55 000 = 330 000 (đồng).
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Phát biểu a) là sai do độ dài đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh đó.
Phát biểu b) là sai do trong một tam giác có ba đường trung bình.
Phát biểu c) là đúng.
Phát biểu d) là sai do đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác đó.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
15 câu Trắc nghiệm Toán 8 Chân trời sáng tạo Bài 1: Đơn thức và đa thức nhiều biến có đáp án
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 25
-
15 câu Trắc nghiệm Toán 8 Cánh diều Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến có đáp án
-
Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 1
-
Đề cuối kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án- Đề 2
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận