Điều hướng LORAN (điều hướng vô tuyến đường dài) cho máy bay và tàu thủy sử dụng các xung đồng bộ được truyền bởi các trạm phát đặt cách xa nhau. Các xung này di chuyển với tốc độ ánh sáng (186 000 dặm/giây). Sự chênh lệch về thời gian nhận được phản xạ của các xung này từ một máy bay hoặc tàu thủy là không đổi, nên máy bay hoặc con tàu sẽ nằm trên một hyperbol có các trạm phát là các tiêu điểm. Giả sử rằng hai trạm phát, cách nhau 300 dặm, được đặt trên một hệ tọa độ vuông góc tại các điểm có tọa độ (–150; 0) và (150; 0) và một con tàu đang đi trên một con đường là một nhánh của hypebol (xem hình vẽ).
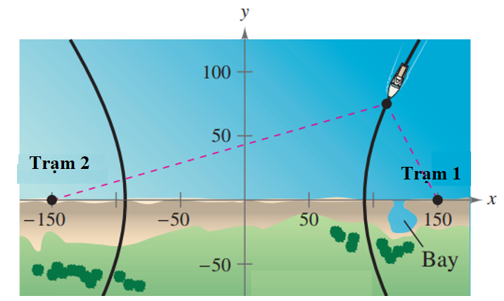
Biết rằng độ chênh lệch thời gian giữa các xung từ các trạm phát với con tàu là 1 000 micro giây (0,001 giây). Khoảng cách giữa tàu và trạm phát số 1 khi tàu vào bờ là
Điều hướng LORAN (điều hướng vô tuyến đường dài) cho máy bay và tàu thủy sử dụng các xung đồng bộ được truyền bởi các trạm phát đặt cách xa nhau. Các xung này di chuyển với tốc độ ánh sáng (186 000 dặm/giây). Sự chênh lệch về thời gian nhận được phản xạ của các xung này từ một máy bay hoặc tàu thủy là không đổi, nên máy bay hoặc con tàu sẽ nằm trên một hyperbol có các trạm phát là các tiêu điểm. Giả sử rằng hai trạm phát, cách nhau 300 dặm, được đặt trên một hệ tọa độ vuông góc tại các điểm có tọa độ (–150; 0) và (150; 0) và một con tàu đang đi trên một con đường là một nhánh của hypebol (xem hình vẽ).

Biết rằng độ chênh lệch thời gian giữa các xung từ các trạm phát với con tàu là 1 000 micro giây (0,001 giây). Khoảng cách giữa tàu và trạm phát số 1 khi tàu vào bờ là
A. 93;
B. 57;
C. 150;
Quảng cáo
Trả lời:
Hướng dẫn giải:
Đáp án đúng là: B
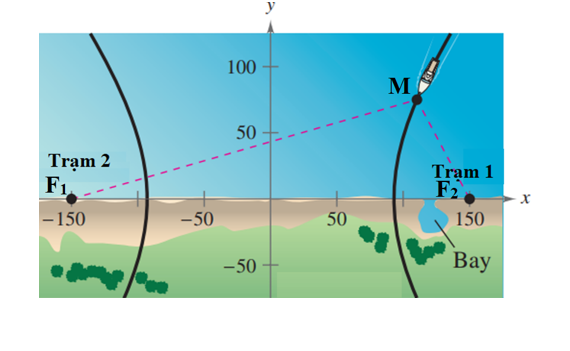
Gọi đường đi của con tàu là (H) thì (H) có phương trình dạng (a, b > 0).
Với giả thiết ta có các tiêu điểm của (H) là F1(–150; 0) và F2(150; 0), suy ra c = 150.
Giả sử vị trí con tàu hiện tại là M(x0; 75) ∈ (H); theo giả thiết độ chênh lệch thời gian giữa các xung từ các trạm phát là 1 000 micro giây (0,001 giây), tức là ta có |MF1 – MF2| = 0,001.186 000 = 186 (dặm); tức là ta có 2a = 186 suy ra a = 93.
Do đó
Phương trình (H) là: .
Trạm phát số 1 nằm tại tiêu điểm F2(150; 0), vị trí khi con tàu vào bờ là đỉnh của (H) là A2(93; 0).
Vậy khoảng cách từ vị trí tàu vào bờ đến trạm số 1 là: F2A2 = 150 – 93 = 57 (dặm).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. 12,8;
B. 5;
C. 1,4;
Lời giải
Hướng dẫn giải:
Đáp án đúng là: D
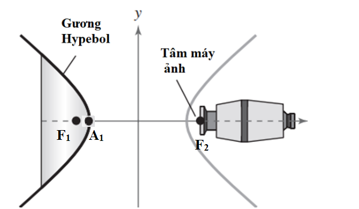
Gọi có a2 = 25 và b2 = 16.
Suy ra .
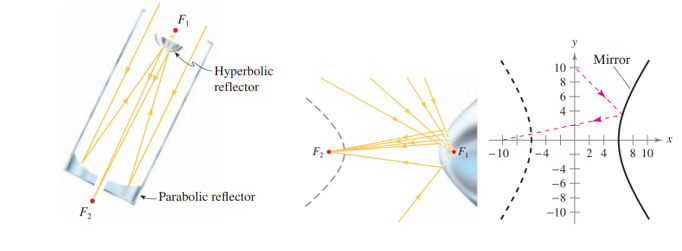
Ta tìm được một tiêu điểm của gương là và đỉnh của gương là A1(–5; 0).
Vậy khoảng cách từ tâm của máy ảnh tới đỉnh của gương là
Câu 2
A. M(6,54; 3,65);
B. M(6,54; 3,55);
C. M(– 32,25; 42,25);
Lời giải
Hướng dẫn giải:
Đáp án đúng là: B
Gọi
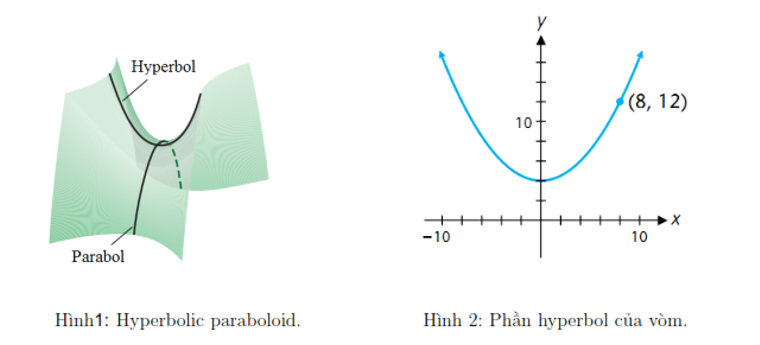
Phương trình của gương (H) có dạng , với a = 6, b = 8;
Suy ra .
Giả sử điểm cần tìm là M ∈ (H).
Gọi đường đi của ánh sáng qua điểm (0; 10) và M là d, do tia sáng sau khi phản xạ bởi gương sẽ đi qua tiêu điểm F1(–10; 0), suy ra d nhằm vào tiêu điểm F2(10; 0) (F2 ∈ d).
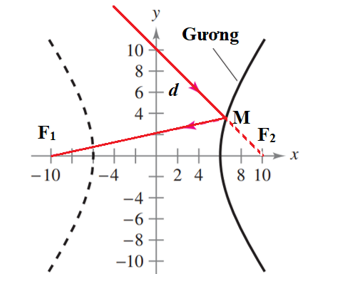
Từ đây dễ dàng lập được phương trình của d là y = –x + 10.
Tọa độ của M ∈ (H) là nghiệm của hệ:
Do điểm cần tìm nằm ở nhánh bên phải nên ta có M(6,54; 3,55).
Câu 3
A. 107,89 km;
B. 167,89 km;
C. 136,01 km;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. 75,00 km;
B. 66,14 km;
C. 100,00 km;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. 2 200;
B. 4 800;
C. 5 280;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.