Một công ty cho thuê thuyền du lịch tính phí thuê thuyền là 1 triệu đồng, ngoài ra tính phí sử dụng 500 nghìn đồng một giờ.

Vẽ đồ thị của hàm số thu được ở câu a để tìm tổng chi phí cho một lần thuê trong 3 giờ.

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

Đồ thị hàm số y = 1 000 + 500x đi qua hai điểm (–2; 0) và (0; 1 000) nên đồ thị hàm số như hình dưới.

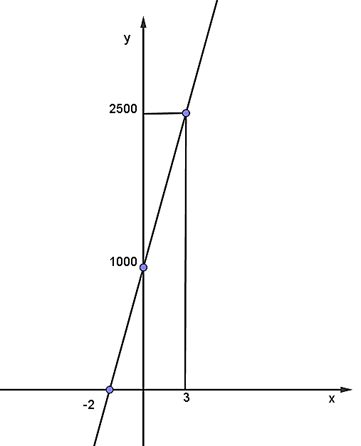
Tổng chi phí cho một lần thuê trong x = 3 giờ tương ứng với điểm y = 2 500 nghìn đồng = 2 triệu 500 nghìn đồng.

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
Đăng ký ngay

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Xem đáp án

Lời giải

Đường thẳng y = mx – 4 cắt đường thẳng y = –2x + 1 tại điểm có hoành độ bằng 2 nên ta có:

m . 2 – 4 = –2 . 2 + 1

2m – 4 = –3

2m = 1

m = \(\frac{1}{2}\) (thỏa mãn).

Vậy m = \(\frac{1}{2}\).

Câu 2

Xem đáp án

Lời giải

Đáp án đúng là: D

Đáp án A không phải phương trình bậc nhất một ẩn vì hệ số của x là 0.

Đáp án B không phải phương trình bậc nhất một ẩn vì:

x – 1 = x + 2

0 = 3

Đáp án C không phải phương trình bậc nhất một ẩn vì x có bậc là 2.

Đáp án D là phương trình bậc nhất một ẩn.

Câu 3