Câu hỏi:

19/08/2025 3,525

Cho đường tròn (O) đường kính AB. Đường thẳng d tiếp xúc với (O) tại A. Gọi I là một điểm cố định trên đoạn thẳng AB. Gọi DE là dây cung thay đổi của (O) luôn đi qua I. Gọi BD, BE cắt d lần lượt tại M, N.

1) Chứng minh rằng tứ giác DENM là tứ giác nội tiếp.

2) Chứng minh rằng tích AM. AN không đổi.

3) Chứng minh rằng tâm đường tròn ngoại tiếp tứ giác DENM thuộc một đường thẳng cố định.

Xem lời giải

Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

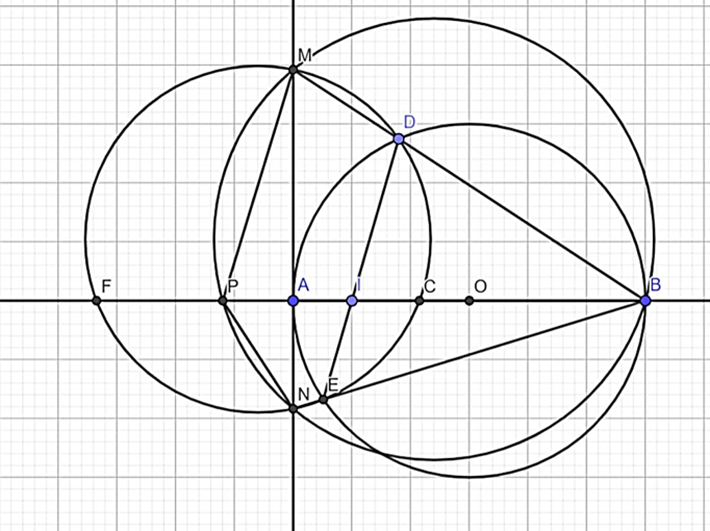
Cho đường tròn (O) đường kính AB. Đường thẳng d tiếp xúc với (ảnh 1)

1) Ta có: AB là đường kính của (O) nên AD ⊥ BM, AE ⊥ EB

Mà AB ⊥ MN

Nên BD.BM = BA² = BE. BN

⇒ \(\frac{{BD}}{{BN}} = \frac{{BE}}{{BM}}\)

Mà \(\widehat {DBE} = \widehat {MBN}\)

⇒ ∆BDE ∽ ∆BNM (c.g.c.)

⇒ \(\widehat {BDE} = \widehat {BNM}\)

⇒ MNED nội tiếp

2) Vẽ đường tròn ngoại tiếp ΔBMN, (BMN) ∩ AB = P

⇒ ΔBEI ∽ ΔBPN(g.g)

⇒ \(\frac{{BE}}{{BP}} = \frac{{BI}}{{BN}}\)

⇒ BI.BP = BE.BN = BA²

⇒ BP = \(\frac{{B{A^2}}}{{BI}}\)⇒ P cố định

Mà \(\widehat {PAN} = \widehat {MAB},\widehat {APN} = \widehat {BPN} = \widehat {BMN} = \widehat {BMA}\)

⇒ ΔABM ∽ ΔANP(g.g)

⇒ \(\frac{{AM}}{{AP}} = \frac{{AB}}{{AN}}\)

⇒ AM.AN = AB. AP không đổi

3.Vẽ đường tròn ngoại tiếp DMNE, (DMNE) ∩ AB = C, F (như hình vẽ)

Chứng minh tương tự câu 2 có AF.AC = AM.AN ⇒ AF.AC = AP.AB

Lại có BCF, BDM là cát tuyến tại B với (DMNE)

⇒ BC.BF = BD.BM = BA²

⇒ \(\left\{ \begin{array}{l}BC.BF = B{A^2}\\AF.AC = AP.AB\end{array} \right.\)

⇒ \(\left\{ \begin{array}{l}\left( {AB - AC} \right)\left( {AB + AF} \right) = B{A^2}\\AF.AC = AP.AB\end{array} \right.\)

⇒ \(\left\{ \begin{array}{l}A{B^2} + AB\left( {AF - AC} \right) - AF.AC = B{A^2}\\AF.AC = AP.AB\end{array} \right.\)

⇒ \(\left\{ \begin{array}{l}AB\left( {AF - AC} \right) = AF.AC\\AF.AC = AP.AB\end{array} \right.\)

⇒ \(\left\{ \begin{array}{l}AB\left( {AF - AC} \right) = AP.AB\\AF.AC = AP.AB\end{array} \right.\)

⇒ \(\left\{ \begin{array}{l}AF - AC = AP\\AF.AC = AP.AB\end{array} \right.\)

⇒ \(\left\{ \begin{array}{l}AF = AC + AP\\AF.AC = AP.AB\end{array} \right.\)

⇒\(\left\{ \begin{array}{l}AF = AC + AP\\A{C^2} + AC.AP - AP.AB = 0\end{array} \right.\) ⇒ C cố định

⇒ C, F cố định

⇒ Tâm (DENM) thuộc trung trực của CF cố định.

Đang tải chế độ Học...

Hot: 1000+ đề thi cuối kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
Đăng ký ngay

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho tam giác nhọn ABC, AB < AC. Các đường cao BE, CF cắt nhau tại H. Gọi M là trung điểm của BC. Trên tia đối của MH lấy điểm K sao cho MH = MK.

a, Chứng minh: BHCK là hình bình hành.

b, Chứng minh: BK vuông góc AB.

c, Chứng minh: tâm giác MEF cân.

d, CQ vuông góc BK tại Q. Chứng minh: EF vuông góc EQ.

Xem đáp án

Lời giải

Cho tam giác nhọn ABC, AB < AC. Các đường cao BE, CF cắt (ảnh 1)

a) Xét tứ giác BHCK có:

M là trung điểm của BC (giả thiết).

M là trung điểm của HK (MH = MK).

⇒ BHCK là hình bình hành (dấu hiệu nhận biết).

b) BHCK là hình bình hành (chứng minh trên).

⇒ BK // HC mà HC ⊥ AB (đường cao)

⇒ AB ⊥ BK (từ vuông góc đến song song đảo).

c) M là trung điểm của BC (giả thiết)

⇒ ME là đường trung tuyến của ΔBCE
Mà ΔBCE vuông tại E ⇒ ME = \(\frac{1}{2}BC\)
M là trung điểm của BC (giả thiết).

⇒ MF là đường trung tuyến của ΔBCF
Mà ΔBCF vuông tại F⇒ MF = \(\frac{1}{2}BC\) = ME
⇒ΔMEF cân (hai cạnh bên bằng nhau).

d) Xét tứ giác BFCQ có:

\(\widehat {BFC} = 90^\circ \)(CF ⊥ AB)

\(\widehat {FBQ} = 90^\circ \)(BK ⊥ AB)

\(\widehat {BQC} = 90^\circ \)(CQ ⊥ BK)

⇒ BFCQ là hình chữ nhật

⇒ BC = FQ

⇒ M là trung điểm FQ

⇒ ME là trung tuyến của tam giác EFQ

Suy ra: ME = \(\frac{1}{2}BC\)= \(\frac{1}{2}PQ\)

⇒ Tam giác EFQ vuông tại E

Vậy EF vuông góc EQ.

Câu 2

Biết đồ thị hàm số y = ax² + bx + c đi qua điểm A(2; 1) và có đỉnh I(1; –1). Tính giá trị biểu thức T = a³ + b² – 2c.

Xem đáp án

Lời giải

Vì đồ thị hàm số y = ax² + bx + c đi qua điểm A(2; 1) và có đỉnh I(1; –1) nên ta có hệ:

\(\left\{ \begin{array}{l}1 = 4a + 2b + c\\ - \frac{b}{{2a}} = 1\\a + b + c = - 1\end{array} \right.\)

⇔ \(\left\{ \begin{array}{l}4a + 2b + c = 1\\ - b = 2a\\a + b + c = - 1\end{array} \right.\)

⇔ \(\left\{ \begin{array}{l} - 2b + 2b + c = 1\\ - 2b = 4a\\a + b + c = - 1\end{array} \right.\)

⇔ \(\left\{ \begin{array}{l}c = 1\\ - 2b = 4a\\a + b + 1 = - 1\end{array} \right.\)

⇔ \(\left\{ \begin{array}{l}c = 1\\4a + 2b = 0\\a + b = - 2\end{array} \right.\)

⇔ \(\left\{ \begin{array}{l}c = 1\\a = 2\\b = - 4\end{array} \right.\)

Khi đó T = a³ + b² – 2c = 2³ + (–4)² – 2.1 = 8 + 16 – 2 = 22.

Câu 3