Câu hỏi:

19/08/2025 743

Cho đường tròn (O) đường kính AB, E thuộc đoạn AO (E khác A, O và AE > EO). Gọi H là trung điểm của AE , kẻ dây CD vuông góc với AE tại H.

a) Tính góc \(\widehat {ACB}\)?

b) Tứ giác ACED là hình gì?

c) Gọi I là giao điểm của DE và BC. Chứng minh HI là tiếp tuyến của đường tròn đường kính EB?

Xem lời giải

Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

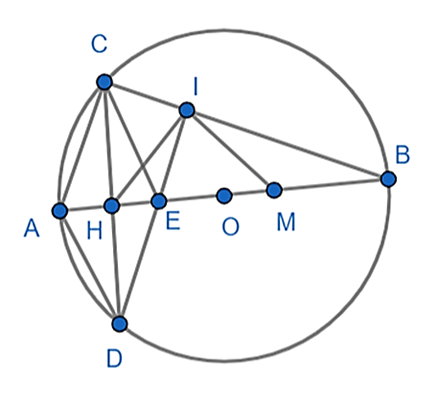
Cho đường tròn (O) đường kính AB, E thuộc đoạn AO (E khác A (ảnh 1)

a) Vì \(\widehat {ACB}\) là góc nội tiếp chắn nửa đường tròn nên \(\widehat {ACB} = 90^\circ \)

b) Xét (O) có:

OH là một phần đường kính

CD là dây

OH ⊥ CD tại H

Do đó: H là trung điểm của CD

Xét tứ giác ECAD có

H là trung điểm của đường chéo CD

H là trung điểm của đường chéo EA

Do đó: ECAD là hình bình hành

Mà EA ⊥ CD

Nên ECAD là hình thoi

c) ACED là hình thoi nên DE //AC

Mà AC ⊥ BC nên DE ⊥ BC

Suy ra: DI ⊥ BC

⇒ \(\widehat {EIB} = 90^\circ ;\widehat {CID} = 90^\circ \)

Xét tam giác CID vuông tại I có IH là trung tuyến

⇒ IH \( = \frac{1}{2}CD = DH\)

⇒ ∆DHI cân tại H ⇒ \(\widehat {HID} = \widehat {EBI}\)

Gọi M là trung điểm BE

Suy ra: IM là trung tuyến của ∆IBE vuông tại I.

⇒ IM = \(\frac{1}{2}BE = BM\)

⇒ ∆MBI cân tại M

⇒ \(\widehat {MBI} = \widehat {MIB} = \widehat {EBI} = \widehat {HID}\)

Ta có: \(90^\circ = \widehat {EIB} = \widehat {B{\mathop{\rm I}\nolimits} M} + \widehat {E{\mathop{\rm I}\nolimits} M} = \widehat {HID} + \widehat {EIM} = \widehat {H{\mathop{\rm I}\nolimits} M}\)

Suy ra: HI ⊥ IM tại I.

Vì IM = EM = BM = \(\frac{1}{2}BE\)và HI ⊥ IM nên HI là tiếp tuyến của \(\left( {M;\frac{{EB}}{2}} \right)\).

Hot: Danh sách các trường đã công bố điểm chuẩn Đại học 2025 (mới nhất) (2025). Xem ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho tam giác nhọn ABC, AB < AC. Các đường cao BE, CF cắt nhau tại H. Gọi M là trung điểm của BC. Trên tia đối của MH lấy điểm K sao cho MH = MK.

a, Chứng minh: BHCK là hình bình hành.

b, Chứng minh: BK vuông góc AB.

c, Chứng minh: tâm giác MEF cân.

d, CQ vuông góc BK tại Q. Chứng minh: EF vuông góc EQ.

Xem đáp án

Lời giải

Cho tam giác nhọn ABC, AB < AC. Các đường cao BE, CF cắt (ảnh 1)

a) Xét tứ giác BHCK có:

M là trung điểm của BC (giả thiết).

M là trung điểm của HK (MH = MK).

⇒ BHCK là hình bình hành (dấu hiệu nhận biết).

b) BHCK là hình bình hành (chứng minh trên).

⇒ BK // HC mà HC ⊥ AB (đường cao)

⇒ AB ⊥ BK (từ vuông góc đến song song đảo).

c) M là trung điểm của BC (giả thiết)

⇒ ME là đường trung tuyến của ΔBCE
Mà ΔBCE vuông tại E ⇒ ME = \(\frac{1}{2}BC\)
M là trung điểm của BC (giả thiết).

⇒ MF là đường trung tuyến của ΔBCF
Mà ΔBCF vuông tại F⇒ MF = \(\frac{1}{2}BC\) = ME
⇒ΔMEF cân (hai cạnh bên bằng nhau).

d) Xét tứ giác BFCQ có:

\(\widehat {BFC} = 90^\circ \)(CF ⊥ AB)

\(\widehat {FBQ} = 90^\circ \)(BK ⊥ AB)

\(\widehat {BQC} = 90^\circ \)(CQ ⊥ BK)

⇒ BFCQ là hình chữ nhật

⇒ BC = FQ

⇒ M là trung điểm FQ

⇒ ME là trung tuyến của tam giác EFQ

Suy ra: ME = \(\frac{1}{2}BC\)= \(\frac{1}{2}PQ\)

⇒ Tam giác EFQ vuông tại E

Vậy EF vuông góc EQ.

Câu 2

Biết đồ thị hàm số y = ax² + bx + c đi qua điểm A(2; 1) và có đỉnh I(1; –1). Tính giá trị biểu thức T = a³ + b² – 2c.

Xem đáp án

Lời giải

Vì đồ thị hàm số y = ax² + bx + c đi qua điểm A(2; 1) và có đỉnh I(1; –1) nên ta có hệ:

\(\left\{ \begin{array}{l}1 = 4a + 2b + c\\ - \frac{b}{{2a}} = 1\\a + b + c = - 1\end{array} \right.\)

⇔ \(\left\{ \begin{array}{l}4a + 2b + c = 1\\ - b = 2a\\a + b + c = - 1\end{array} \right.\)

⇔ \(\left\{ \begin{array}{l} - 2b + 2b + c = 1\\ - 2b = 4a\\a + b + c = - 1\end{array} \right.\)

⇔ \(\left\{ \begin{array}{l}c = 1\\ - 2b = 4a\\a + b + 1 = - 1\end{array} \right.\)

⇔ \(\left\{ \begin{array}{l}c = 1\\4a + 2b = 0\\a + b = - 2\end{array} \right.\)

⇔ \(\left\{ \begin{array}{l}c = 1\\a = 2\\b = - 4\end{array} \right.\)

Khi đó T = a³ + b² – 2c = 2³ + (–4)² – 2.1 = 8 + 16 – 2 = 22.

Câu 3