Câu hỏi:
13/07/2024 2,173
Cho tam giác ABC, kẻ tia phân giác Bx của góc B, Bx cắt tia AC tại M. Từ M kẻ đường thẳng song song với AB, nó cắt BC tại N. Từ N kẻ tia NY // Bx. Chứng minh:
a. \(\widehat {xAB} = \widehat {BMN}\).
b. Tia Ny là tia phân giác của góc MNC.
Cho tam giác ABC, kẻ tia phân giác Bx của góc B, Bx cắt tia AC tại M. Từ M kẻ đường thẳng song song với AB, nó cắt BC tại N. Từ N kẻ tia NY // Bx. Chứng minh:
a. \(\widehat {xAB} = \widehat {BMN}\).
b. Tia Ny là tia phân giác của góc MNC.
Quảng cáo
Trả lời:
Giải bởi Vietjack
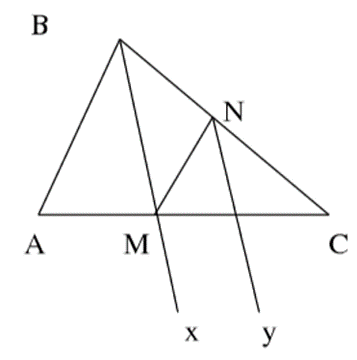
a) Trong tam giác ABC tại đỉnh B có:
\(\widehat {ABx\;} = \widehat {xBC}\)(vì Bx là tia phân giác của góc B)
\(\widehat {BMN} = \widehat {ABx}\)(2 góc so le trong vì MN//BA)
Vậy \(\widehat {BMN} = \widehat {xBC}\).
b) \[\widehat {BMN\;} = \widehat {MNy}\](2 góc so le trong vì Ny//Bx)
\(\widehat {xBC} = \widehat {yNC}\)(2 góc đồng vị vì Ny//Bx)
Vậy \[\widehat {yNC} = \widehat {MNy}\]mà tia Ny là tia nằm giữa hai tia MN và NC
Do đó: Ny là tia phân giác của MNC.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
\(\tan \left( {\alpha - \frac{\pi }{4}} \right) = \frac{{\tan \alpha - \tan \frac{\pi }{4}}}{{1 + \tan \alpha .\tan \frac{\pi }{4}}} = \frac{{2 - 1}}{{2 + 1}} = \frac{1}{3}\).
Lời giải
Tính được: 270° = \(\frac{{270}}{{180}}\pi = \frac{3}{2}\pi = \frac{3}{4}.2\pi \)
Vậy đu quay được góc 270° khi nó quay được \(\frac{3}{4}\) vòng
Ta có: đu quay quay được 1 vòng trong \(\frac{1}{3}\) phút
Vậy đu quay đu được \(\frac{3}{4}\) vòng trong: \(\frac{3}{4}.\frac{1}{3} = \frac{1}{4}\) phút.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo