Cho hình vẽ biết : Ax // By, xAO^=32°,OBy^=122°. Chứng tỏ OA vuông góc với OB.

Theo giả thiết: Ax // By; xAO^=32°,OBy^=122° Kẻ tia Oz song song với Ax song song với By ⇒ OBy^+BOz^=180° ( vì là 2 góc trong cùng phía ) ⇒ BOz^=180°−OBy^=180°−122°=58° Mà ta có Ax // Oz ⇒ AOz^=xAO^=32° ( vì là 2 góc so le trong bằng nhau ) ⇒ AOB^=AOz^+BOz^=32°+58°=90° ⇒ AOB^ là góc vuông ⇒ OA vuông góc với OB.

Câu hỏi:

19/08/2025 3,793

Cho hình vẽ biết : Ax // By, $\hat{x A O} = 32 °, \hat{O B y} = 122 °$ . Chứng tỏ OA vuông góc với OB.

Xem lời giải

Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

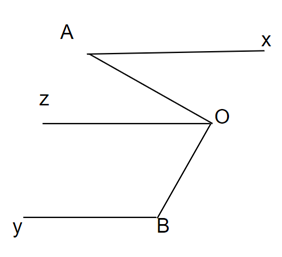
Cho hình vẽ biết : Ax // By, góc xAO = 32 độ, góc OBy = 122 độ. Chứng tỏ OA vuông góc với OB. (ảnh 2)

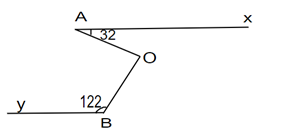
Theo giả thiết: Ax // By; $\hat{x A O} = 32 °, \hat{O B y} = 122 °$

Kẻ tia Oz song song với Ax song song với By

⇒ $\hat{O B y} + \hat{B O z} = 180 °$ ( vì là 2 góc trong cùng phía )

⇒ $\hat{B O z} = 180 ° - \hat{O B y} = 180 ° - 122 ° = 58 °$

Mà ta có Ax // Oz

⇒ $\hat{A O z} = \hat{x A O} = 32 °$ ( vì là 2 góc so le trong bằng nhau )

⇒ $\hat{A O B} = \hat{A O z} + \hat{B O z} = 32 ° + 58 ° = 90 °$

⇒ $\hat{A O B}$ là góc vuông

⇒ OA vuông góc với OB.

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

Các sản phẩm khác của Vietjack:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hình thang cân ABCD có AB // CD, O là giao điểm của hai đường chéo, E là giao điểm của hai đường thẳng chứa hai cạnh bên AD và BC. Chứng minh: OA = OB; OC = OD.

Xem đáp án

Lời giải

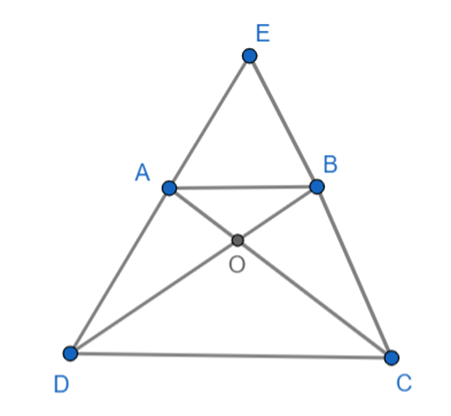
Cho hình thang cân ABCD có AB // CD, O là giao điểm của hai đường chéo, E là giao điểm của hai đường thẳng chứa hai cạnh bên AD và BC. Chứng minh: OA = OB; OC = OD. (ảnh 1)

Xét ∆ADC và ∆BCD, ta có:

AD = BC (tính chất hình thang cân)

$\hat{A D C} = \hat{B C D}$ (gt)

DC chung

Do đó: ∆ADC = ∆BCD (c.g.c) ⇒ $\hat{A C D} = \hat{B D C}$

Trong ∆OCD ta có: $\hat{A C D} = \hat{B D C}$

⇒ ∆OCD cân tại O

⇒ OC = OD (1)

AC = BD (tính chất hình thang cân)

⇒ AO + OC = BO + OD (2)

Từ (1) và (2) suy ra: AO = BO.

Vậy OA = OB; OC = OD.

b) Theo phần a có: OA = OB

∆ADC = ∆BCD (c.g.c)

⇒ ∆EDC cân tại E

⇒ EC = ED nên E thuộc đường trung trực CD

OC = OD nên O thuộc đường trung trực CD

E ≠ O. Vậy OE là đường trung trực của CD.

Ta có: BD= AC (tính chất hình thang cân)

⇒ EB + ED = EA + EC mà ED = EC

⇒ EB = EA nên E thuộc đường trung trực AB

OA = OB (chứng minh trên ) nên O thuộc đường trung trực của AB

E ≠ O. Vậy OE là đường trung trực của AB.

Câu 2

Cho dãy số 1, 2, 3, 4, ..., 199, 200; hỏi dãy số có bao nhiêu số chẵn, bao nhiêu số lẻ?

Xem đáp án

Lời giải

Tổng số hạng của dãy là:

(200 – 1) : 1 + 1 = 200 (số hạng)

Số lẻ bắt đầu từ 1 và kết thúc là 199, mỗi số lẻ cách nhau 2 đơn vị

Số các số lẻ là:

(199 – 1) : 2 + 1 = 100 (số lẻ)

Số các số chẵn là:

200 – 100 = 100 (số chẵn).

Câu 3