Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta thấy từng số hạng của M đều chia hết cho 2
Nên M = 2 + 22 + 23 + … + 220 chia hết cho 2 (1)
Lại có: M = 2 + 22 + 23 + … + 220
M = (2 + 23) + (22 + 24) + … + (217 + 219) + (218 + 220)
M = 2(1 + 22) + 22(1 + 22) + … + 217(1 + 22) + 218(1 + 22)
M = (1 + 22)(2 + 22 + … + 217 + 218)
M = 5.(2 + 22 + … + 217 + 218) ⋮ 5 (2)
Từ (1) và (2) suy ra: M chia hết cho 10.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
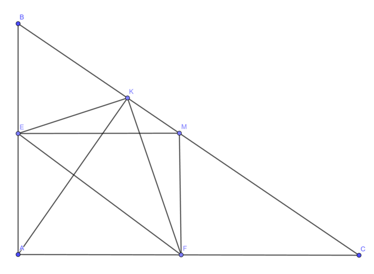
a. Tứ giác AEFM có 3 góc vuông nên AEFM là hình chữ nhật
b. ΔABC là tam giác vuông tại A, có AM là đường trung tuyến nên AM = MC = MB
ΔCMA là tam giác cân tại M (do MC = MA) nên MF là đường cao cũng là đường trung tuyến
⇒ F là trung điểm AC (1)
ΔBMA là tam giác cân tại M (do MA = MB) nên ME là đường cao cũng là đường trung tuyến
⇒ E là trung điểm AB (2)
Từ (1) và (2) suy ra: EF là đường trung bình của ΔABC
⇒ EF = BC (đpcm)
c, EF là đường trung bình của ΔABC ⇒ EF // BC
⇒ Tứ giác EKMF là hình thang
ΔAKC vuông tại K có KF là trung tuyến ứng với cạnh huyền
⇒ KF = FA mà FA = ME (do AEMF là hình chữ nhật)
⇒ KF = ME
⇒ Hình thang EKMF là hình thang cân (đpcm).
Lời giải
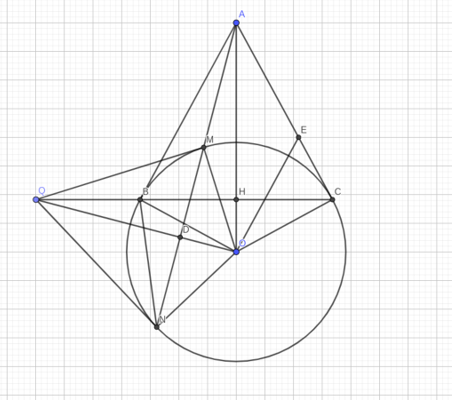
a. Vì AB, AC là tiếp tuyến của (O)
⇒ AO ⊥ BC = H
b. Ta có: OE ⊥ OB
⇒ OE // AB vì AB là tiếp tuyến của (O)
⇒ OB ⊥ AB
⇒
⇒ΔOAE cân tại E
c.Ta có : AB,AC là tiếp tuyến của (O)
⇒ OB ⊥ AB mà BC⊥AB = H
⇒ OH.OA = OB2 = R2
Tương tự QM, QN là tiếp tuyến của (O)
Gọi QO ∩ MN = D
⇒ OD.OQ = OM2 = R2 vì OM ⊥ QM
⇒ OH.OA = OD.OQ
⇒
⇒ΔODA ∽ ΔOHQ(c.g.c)
⇒ AD ⊥ OQ
Mà MN ⊥ OQ = D
⇒ A, M, D, N thẳng hàng
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)