Cho hình bình hành ABCD, hai đường chéo cắt nhau ở O. Hai đường thẳng d1 và d2 cùng đi qua O và vuông góc với nhau. Đường thẳng d1 cắt các cạnh AB và CD ở M và P. Đường thẳng d2 cắt các cạnh BC và AD ở N và Q.
a/ Chứng minh tứ giác MNPQ là hình thoi.
b/ Nếu ABCD là hình vuông thì tứ giác MNPQ là hình gì? Hãy chứng minh.
Cho hình bình hành ABCD, hai đường chéo cắt nhau ở O. Hai đường thẳng d1 và d2 cùng đi qua O và vuông góc với nhau. Đường thẳng d1 cắt các cạnh AB và CD ở M và P. Đường thẳng d2 cắt các cạnh BC và AD ở N và Q.
a/ Chứng minh tứ giác MNPQ là hình thoi.
b/ Nếu ABCD là hình vuông thì tứ giác MNPQ là hình gì? Hãy chứng minh.
Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
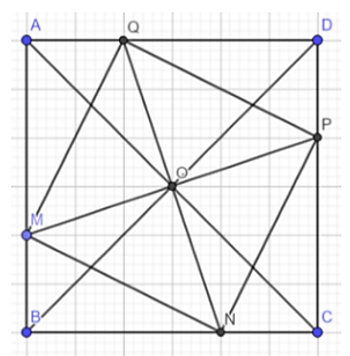
a/ Ta có ABCD là hình bình hành nên AC cắt BD tại trung điểm O mỗi đường
Nên OA = OC; OB = OD
Mà AB // CD nên
Nên OM = OP hay O là trung điểm MP
Tương tự: O là trung điểm NQ
Vì d1 vuông góc d2 tức NQ vuông góc MP
Suy ra: NQ ⊥ MP = O là trung điểm mỗi đường
Vậy MNPQ là hình thoi
b/ Nếu ABCD là hình vuông thì AC ⊥ BD
Suy ra:
Mà OB = OC;
Xét tam giác OBM và tam giác OCN có:
OB = OC
Nên: ∆OBM = ∆OCN (g.c.g)
Suy ra: OM = ON
Kết hợp phần a nên MNPQ là hình vuông.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
(P) đi qua A(-1; 0) nên: 0 = a – b + c
⇔ c = b - a (1)
(P) đi qua đỉnh B(1; 2) nên:
2 = a + b + c
Vậy T = a + b + c = 2.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
(a + b + c)3
= [(a + b) + c]3
= (a + b)3 + c3 + 3(a + b)c(a + b + c)
= a3 + b3 + 3ab(a + b) + c3 + 3(a + b)c(a + b + c)
= a3 + b3 + c3 + 3ab(a + b) + 3(a + b)c(a + b + c)
= a3 + b3 + c3 + 3(a + b)(ab + ac + bc + c2)
= a3 + b3 + c3 + 3(a + b)(b + c)(c + a).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập