Câu hỏi:
12/07/2024 26,164
Một hộp quà có dạng là một hình chóp tứ giác đều có cạnh đáy bằng 10 cm, trung đoạn bằng 13 cm. Tính chiều cao của hộp quà.
Câu hỏi trong đề:
Đề kiểm tra Cuối kì 2 Toán 8 KNTT có đáp án !!
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
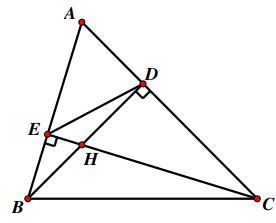
Ta có SE là trung đoạn nên E là trung điểm của AB .
Xét có E, H lần lượt là trung điểm của AB, BD .
Suy ra EH là đường trung bình của nên .
Áp dụng định lí Pythagore vuông tại H có:
Suy ra
Do đó .
Vậy chiều cao của hộp quà là 12 cm.
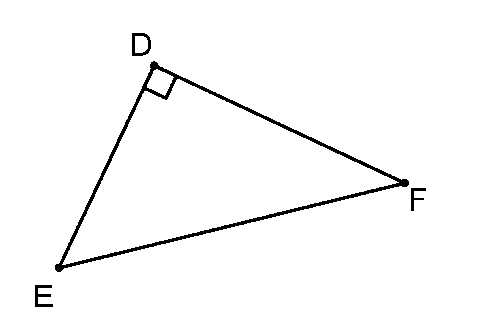
a) Xét và có
;
Do đó .
b) Từ câu a: suy ra .
Do đó
Vậy AE = 2,5 cm
c) Từ câu a: suy ra hay .
Xét và có:
; (cmt)
Do đó
Suy ra (hai góc tương ứng) (1)
Mặt khác, ta có:
• (2)
• (3)
Từ (1), (2) và (3) nên suy ra
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 4:
Một đội thanh niên tình nguyện gồm 11 thành viên đến từ các tỉnh, TP như sau: Kon Tum; Bình Phước; Tây Ninh; Bình Dương; Gia Lai; Bà Rịa – Vũng Tàu; Đồng Nai; Đăk Lăk ; Đăk Nông; Lâm Đồng; TP Hồ Chí Minh, mỗi tỉnh, TP chỉ có đúng một thành viên trong đội. Chọn ngẫu nhiên một thành viên của đội tình nguyện đó.
a) Gọi K là tập hợp gồm các kết quả có thể xảy ra đối với thành viên được chọn. Tính số phần tử của tập hợp K.
b) Tính xác suất của mỗi biến cố sau :
− “Thành viên được chọn ra đến từ vùng Tây Nguyên”.
− “Thành viên được chọn ra đến từ vùng Đông Nam Bộ”.
Xem đáp án »
12/07/2024
4,243
Câu 5:
Cho tam giác DEF vuông tại D Biểu thức nào đúng trong các biểu thức sau?
Cho tam giác DEF vuông tại D Biểu thức nào đúng trong các biểu thức sau?
Xem đáp án »
08/03/2024
3,860
Câu 6:
Sử dụng quy tắc đổi dấu, ta đưa phân thức về dạng phân thức nào sau đây?
Sử dụng quy tắc đổi dấu, ta đưa phân thức về dạng phân thức nào sau đây?
Xem đáp án »
08/03/2024
3,460
Bình luận
🔥 Đề thi HOT:
-
10 Bài tập Bài toán thực tiễn gắn với việc vận dụng định lí Thalès (có lời giải)
-
10 Bài tập Các bài toán thực tiễn gắn với việc vận dụng định lí Pythagore (có lời giải)
-
15 câu Trắc nghiệm Toán 8 KNTT Bài 1: Đơn thức có đáp án
-
Bài tập Nhân đơn thức với đa thức (có lời giải chi tiết)
-
Đề kiểm tra Cuối kì 1 Toán 8 KNTT có đáp án (Đề 1)
-
10 Bài tập Các bài toán thực tiễn gắn với việc vận dụng định lí Pythagore (có lời giải)
-
10 Bài tập Bài toán thực tiễn gắn với việc vận dụng định lí Thalès (có lời giải)
-
10 Bài tập Bài toán thực tiễn liên quan đến thể tích, diện tích xung quanh của hình chóp tứ giác đều (có lời giải)
về câu hỏi!