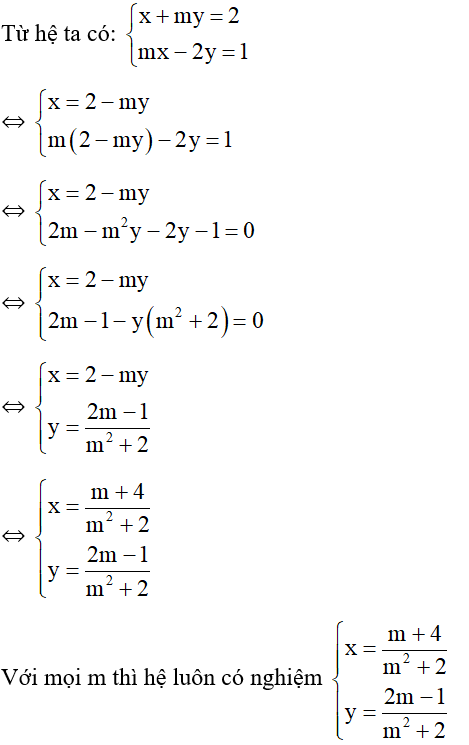Cho hàm số y= f(x). Đồ thị hàm số y= f’(x) như hình dưới và f(-2) = f( 2) = 0.
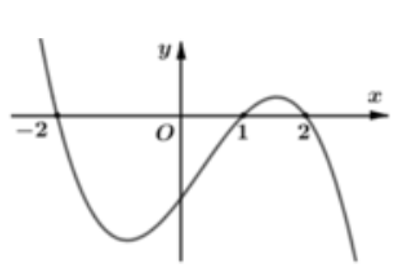
Hàm số g( x) = [f(3 - x)]2 nghịch biến trên khoảng nào trong các khoảng sau?
A. (- 2; -1).
B. (1; 2).
C. (2; 5).
D. ( 5 ; +∞).
Quảng cáo
Trả lời:
Chọn C.
Dựa vào đồ thị hàm số y = f’(x) suy ra bảng biến thiên của hàm số y = f(x)
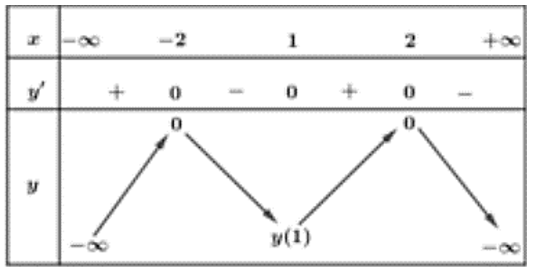
Suy ra: f(x) ≤ 0 với mọi x
Ta có: g’(x) = -2f’(3 – x).f(3 – x)
Xét g’(x) < 0 thì f’(3 – x).f(3 – x) > 0
⇔
Suy ra hàm số y = g(x) nghịch biến trên các khoảng (2; 5) và (-∞; 1).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
(P) đi qua A(-1; 0) nên: 0 = a – b + c
⇔ c = b - a (1)
(P) đi qua đỉnh B(1; 2) nên:
2 = a + b + c
Vậy T = a + b + c = 2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.