Biểu đồ dưới đây thống kê thời gian tập thể dục buổi sáng mỗi ngày trong tháng 9/2022 của bác Bình và bác An.
Ai là người có thời gian tập đều hơn?
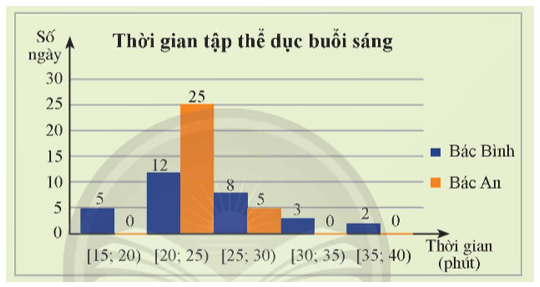
Biểu đồ dưới đây thống kê thời gian tập thể dục buổi sáng mỗi ngày trong tháng 9/2022 của bác Bình và bác An.
Ai là người có thời gian tập đều hơn?

Quảng cáo
Trả lời:
Sau bài học này, ta giải quyết được bài toán trên như sau:
Từ biểu đồ đã cho, ta có bảng thống kê sau:
|
Thời gian (phút) |
[15; 20) |
[20; 25) |
[25; 30) |
[30; 35) |
[35; 40) |
|
Số ngày tập của bác Bình |
5 |
12 |
8 |
3 |
2 |
|
Số ngày tập của bác An |
0 |
25 |
5 |
0 |
0 |
Khoảng biến thiên của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng của bác Bình là 40 – 15 = 25 (phút).
Tuy nhiên, trong mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng của bác An, khoảng đầu tiên chứa dữ liệu là [20; 25) và khoảng cuối cùng chứa dữ liệu là [25; 30).
Do đó, khoảng biến thiên của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng của bác An là 30 – 20 = 10 (phút).
Nếu căn cứ theo khoảng biến thiên thì bác Bình có thời gian tập thể dục phân tán hơn bác An, vậy bác An là người có thời gian tập đều hơn.
Cỡ mẫu n = 30.
- Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng mỗi ngày của bác Bình:
Gọi x1; x2; …; x30 là mẫu số liệu gốc về thời gian tập thể dục buổi sáng mỗi ngày của bác Bình được xếp theo thứ tự không giảm.
Ta có x1; x2; …; x5 ∈ [15; 20), x6; x7; …; x17 ∈ [20; 25),
x18; x19; …; x25 ∈ [25; 30), x26; …; x28 ∈ [30; 35), x29; x30 ∈ [35; 40).
Tứ phân vị thứ nhất Q1 của mẫu số liệu gốc là x8 ∈ [20; 25). Do đó, tứ phân thứ nhất của mẫu số liệu ghép nhóm là .
Tứ phân vị thứ ba Q3 của mẫu số liệu gốc là x23 ∈ [25; 30). Do đó, tứ phân thứ ba của mẫu số liệu ghép nhóm là .
Khoảng tứ phân vị của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng mỗi ngày của bác Bình là ∆Q = Q3 – Q1 = .
- Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng mỗi ngày của bác An:
Gọi y1; y2; …; y30 là mẫu số liệu gốc về thời gian tập thể dục buổi sáng mỗi ngày của bác An được xếp theo thứ tự không giảm.
Ta có y1; y2; …; y25 ∈ [20; 25), y26; …; y29; y30 ∈ [25; 30).
Tứ phân vị thứ nhất Q'1 của mẫu số liệu gốc là y8 ∈ [20; 25). Do đó, tứ phân thứ nhất của mẫu số liệu ghép nhóm là .
Tứ phân vị thứ ba Q'3 của mẫu số liệu gốc là y23 ∈ [20; 25). Do đó, tứ phân thứ ba của mẫu số liệu ghép nhóm là .
Khoảng tứ phân vị của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng mỗi ngày của bác An là ∆'Q = Q'3 – Q'1 = .
Vì ∆Q = ≈ 7,4 > ∆'Q = 3 nên khoảng tứ phân vị của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng mỗi ngày của bác Bình lớn hơn bác An.
Vậy nếu căn cứ theo khoảng tứ phân vị thì bác An là người có thời gian tập đều hơn.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Khoảng biến thiên của mẫu số liệu ghép nhóm là:
R = 9,4 – 8,4 = 1 (m).
Cỡ mẫu n = 100.
Gọi x1; x2; …; x100 là mẫu số liệu gốc về chiều cao của 100 cây keo 3 năm tuổi tại một nông trường được xếp theo thứ tự không giảm.
Ta có x1; …; x5 ∈ [8,4; 8,6), x6; …; x17 ∈ [8,6; 8,8), x18; …; x42 ∈ [8,8; 9,0),
x43; …; x86 ∈ [9,0; 9,2), x87; …; x100 ∈ [9,2; 9,4).
Tứ phân vị thứ nhất của mẫu số liệu gốc là ∈ [8,8; 9,0).
Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: .
Tứ phân vị thứ ba của mẫu số liệu gốc là ∈ [9,0; 9,2).
Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:.
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là:
∆Q = Q3 – Q1 = 9,15 – 8,864 = 0,286.
b) Trong 100 cây keo trên có 1 cây cao 8,4 m thuộc nhóm [8,4; 8,6).
Vì Q1 – 1,5∆Q = 8,864 – 1,5 ∙ 0,286 = 8,435 > 8,4 nên chiều cao của cây keo cao 8,4 m là giá trị ngoại lệ của mẫu số liệu ghép nhóm.
Lời giải
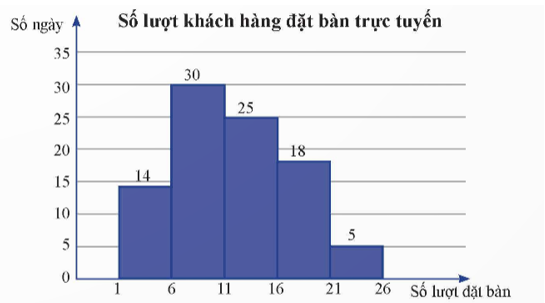
Từ biểu đồ đã cho, ta có có bảng thống kê sau:
|
Số lượt đặt bàn |
[1; 6) |
[6; 11) |
[11; 16) |
[16; 21) |
[21; 26) |
|
Số ngày |
14 |
30 |
25 |
18 |
5 |
Cỡ mẫu n = 14 + 30 + 25 + 18 + 5 = 92.
Gọi x1; x2; …; x92 là mẫu số liệu gốc về số lượt khách đặt bàn qua hình thức trực tuyến mỗi ngày trong quý III năm 2022 của một nhà hàng được xếp theo thứ tự không giảm.
Ta có x1; …; x14 ∈ [1; 6), x15; …; x44 ∈ [6; 11), x45; …; x69 ∈ [11; 16),
x70; …; x87 ∈ [16; 21), x88; …; x92 ∈ [21; 26).
Tứ phân vị thứ nhất của mẫu số liệu gốc là ∈ [6; 11).
Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: = 7,5.
Tứ phân vị thứ ba của mẫu số liệu gốc là .
Mà x69 ∈ [11; 16) và x70 ∈ [16; 21)
Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là Q3 = 16.
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là:
∆Q = Q3 – Q1 = 16 – 7,5 = 8,5.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.