Tính giới hạn $\mathop {\lim }\limits_{x \to 1} \frac{{2\sqrt {x + 3} + x - 5}}{{x - {x^2}}}$.

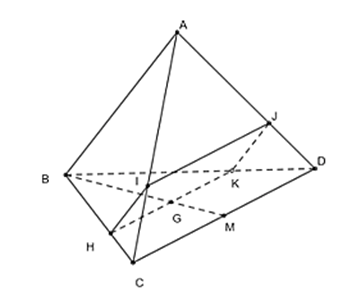
a) Gọi $\Delta $ là giao tuyến của $\left( P \right)$ và $\left( {BCD} \right)$. Khi đó $\Delta $ đi qua $G$ và song song với $CD$.

Gọi $H,K$ lần lượt là giao điểm của $\Delta $ với $BC$ và $BD$.

\[ \Rightarrow \left\{ {\begin{array}{*{20}{c}}

{H \in \left( P \right)} \\

{H \in BC \subset \left( {BCD} \right)}

\end{array}} \right. \Rightarrow H \in \left( P \right) \cap \left( {BCD} \right)(1)\]                                                                       

\[ \Rightarrow \left\{ {\begin{array}{*{20}{c}}

{K \in \left( P \right)} \\

{K \in BD \subset \left( {BCD} \right)}

\end{array}} \right. \Rightarrow K \in \left( P \right) \cap \left( {BCD} \right)(2)\]

Từ \[\left( 1 \right),\left( 2 \right)\] suy ra giao tuyến của $\left( P \right)$ và $\left( {BCD} \right)$ là $HK$.

b) Vì $G$ là trọng tâm tam giác $BCD$ và $HK{\text{//}}CD$ nên $\frac{{CH}}{{CB}} = \frac{{MG}}{{MB}} = \frac{{DK}}{{DB}} = \frac{1}{3}$.

Giả sử $\left( P \right)$ cắt $\left( {ABC} \right)$ và $\left( {ABD} \right)$ các giao tuyến là $HI$ và $KJ$.

Ta có \[\left( P \right) \cap \left( {ABC} \right) = HI\], \[\left( P \right) \cap \left( {ABD} \right) = KJ\,\] mà \[AB\parallel \left( P \right)\] nên \[HI\parallel AB\parallel KJ\].

Theo định lí Thalès, ta có \[\frac{{BH}}{{HC}} = \frac{{BK}}{{KD}} = \frac{{BG}}{{GM}} = 2\] suy ra $\left\{ \begin{gathered}

\frac{{HI}}{{AB}} = \frac{{CH}}{{CB}} = \frac{1}{3} \hfill \\

\frac{{KJ}}{{AB}} = \frac{{DK}}{{DB}} = \frac{1}{3} \hfill \\

\end{gathered} \right. \Rightarrow HI = KJ$.

Vậy thiết diện của \[\left( P \right)\] và tứ diện \[ABCD\] là hình bình hành $HIJK$.