Đề kiểm tra Cuối kì 1 Toán 11 Kết nối tri thức có đáp án
75 người thi tuần này 4.6 1.3 K lượt thi 39 câu hỏi 90 phút
🔥 Đề thi HOT:
Bài tập Hình học không gian lớp 11 cơ bản, nâng cao có lời giải (P11)
Bài tập Lượng giác lớp 11 cơ bản, nâng cao có lời giải (P1)
105 Bài tập trắc nghiệm Tổ hợp - Xác suất từ đề thi đại học có lời giải (P1)
12 câu Trắc nghiệm Toán 11 Kết nối tri thức Giá trị lượng giác của góc lượng giác có đáp án
17 bài trắc nghiệm Lượng giác từ đề thi Đại học cực hay có lời giải chi tiết (P1)
14 Bài tập Giới hạn cực hay có lời giải chi tiết (P1)
45 Bài tập Đạo Hàm cực hay có lời giải chi tiết (P1)
15 câu lượng giác cơ bản , nâng cao (có đáp án) (p1)
Nội dung liên quan:
Danh sách câu hỏi:
Câu 1
B. $\sin \alpha = {x_0}$.
D. $\sin \alpha = - {y_0}$.
Lời giải
Chọn A
Câu 2
Lời giải
Chọn D
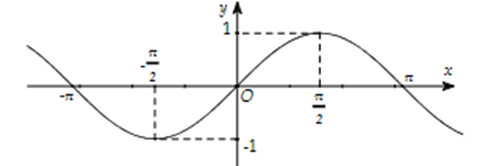
Câu 3
B. Hàm số nghịch biến trên $\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)$.
D. Hàm số đồng biến trên $\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)$.
Lời giải
Chọn D
Câu 4
B. $\left[ \begin{gathered}
x = \arcsin \frac{3}{2} + k2\pi \hfill \\
x = \pi - \arcsin \frac{3}{2} + k2\pi \hfill \\
\end{gathered} \right.\left( {k \in \mathbb{Z}} \right)$.
C. $\left[ \begin{gathered}
x = \arcsin \frac{3}{2} + k2\pi \hfill \\
x = - \arcsin \frac{3}{2} + k2\pi \hfill \\
\end{gathered} \right.\left( {k \in \mathbb{Z}} \right)$.D. $x \in \mathbb{R}$.
Lời giải
Chọn A
Câu 5
B. $x = - \frac{\pi }{4} + k2\pi ,k \in \mathbb{Z}$.
D. $x = - \frac{\pi }{4} + k\pi ,k \in \mathbb{Z}$.
Lời giải
Chọn D
Câu 6
B. ${u_n} = {\left( { - 1} \right)^n}\left( {{5^n} - 1} \right)$.
D. ${u_n} = \sqrt {n + 4} $.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
B. Bị chặn trên.
D. Không bị chặn dưới.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
B. ${u_1} = 1;{u_2} = \frac{5}{4};{u_3} = \frac{7}{5};{u_4} = \frac{3}{2};{u_5} = \frac{{11}}{7}$.
D. ${u_1} = 1;{u_2} = \frac{5}{4};{u_3} = \frac{7}{5};{u_4} = \frac{7}{2};{u_5} = \frac{{11}}{3}$.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
B. ${u_n} = 3n + 2008$.
D. ${u_n} = {\left( { - 3} \right)^{n + 1}}$.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
D. $d = \frac{3}{{11}}$.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
D. ${u_n} = 2 + 3n$.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
B. Số hạng tổng quát ${u_n} = {1^n} = 1$.
D. Số hạng tổng quát ${u_n} = {\left( { - 1} \right)^{2n}}$.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 17
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 18
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 19
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 20
D. $\mathop {\lim }\limits_{x \to - {1^ + }} \frac{{3x + 2}}{{x + 1}} = - \infty $.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 21
D. $f\left( x \right) = \frac{{x + 1}}{{x - 1}}$.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 22
B. $f\left( x \right) = \frac{{{x^2} + 3}}{{5 - x}}$.
D. $f\left( x \right) = \frac{{x + 5}}{{{x^2} + 4}}$.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 23
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 24
A. Hai mặt phẳng có một điểm chung thì chúng còn có vô số điểm chung khác nữa.
C. Hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất.
D. Nếu ba điểm phân biệt $M,N,P$ cùng thuộc hai mặt phẳng phân biệt thì chúng thẳng hàng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 25
D. 14.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 26
A. $AK$, $K$ là giao điểm của $IJ$ và $BC$.
B. $AH$, $H$ là giao điểm của $IJ$ và $AB$.
C. $AG$, $G$ là giao điểm của $IJ$ và $AD$.
D. $AF$, $F$ là giao điểm của $IJ$ và $CD$.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 28
D. Đường thẳng $SA$.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 29
Cho đường thẳng $d$ song song với mặt phẳng $\left( P \right)$. Mệnh đề nào sau đây đúng?
C. Đường thẳng $d$ có đúng hai điểm chung với mặt phẳng $\left( P \right)$.
C. Đường thẳng $d$ có đúng hai điểm chung với mặt phẳng $\left( P \right)$.
D. Đường thẳng $d$ có vô số điểm chung với mặt phẳng $\left( P \right)$.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 30
B. Mặt phẳng $\left( {ACD} \right)$.
D. Mặt phẳng $\left( {BCD} \right)$.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 31
B. $MN{\text{//}}BD$.
D. $MN$ cắt $BC$.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 32
A. Nếu hai mặt phẳng $\left( \alpha \right)$ và $\left( \beta \right)$ song song với nhau thì mọi đường thẳng nằm trong $\left( \alpha \right)$ đều song song với $\left( \beta \right)$.
B. Nếu hai mặt phẳng $\left( \alpha \right)$ và $\left( \beta \right)$ song song với nhau thì bất kì đường thẳng nào nằm trong $\left( \alpha \right)$ cũng song song với bất kì đường thẳng nào nằm trong $\left( \beta \right)$.
C. Nếu hai đường thẳng phân biệt $a$ và $b$ song song lần lượt nằm trong hai mặt phẳng $\left( \alpha \right)$ và $\left( \beta \right)$ phân biệt thì $\left( \alpha \right){\text{//}}\left( \beta \right)$.
D. Nếu đường thẳng $d$ song song với $\left( \alpha \right)$ thì nó song song với mọi đường thẳng nằm trong $\left( \alpha \right)$.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
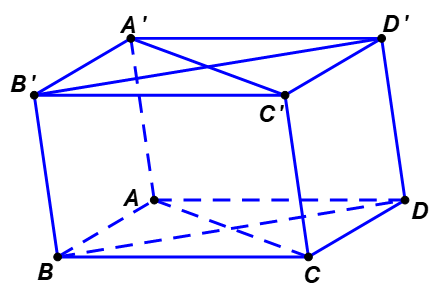
Câu 33
B. $\left( {AA'D'D} \right)\;{\text{//}}\;\left( {BCC'B'} \right)$.
D. $\left( {ABB'A'} \right)\;{\text{//}}\;\left( {CDD'C'} \right)$.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 34
B. Một đường thẳng.
D. Cả ba trường hợp trên.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 35
B. $\left( \alpha \right) \equiv \left( P \right)$.
D. Cả A, B, C đều sai.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.