Câu hỏi:
12/07/2024 571
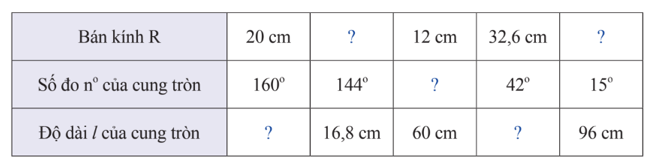
b) Gọi H là trung điểm của AC. Vẽ dây DE của (O) vuông góc với AC tại H. Chứng minh tứ giác ADCE là hình thoi.
b) Gọi H là trung điểm của AC. Vẽ dây DE của (O) vuông góc với AC tại H. Chứng minh tứ giác ADCE là hình thoi.
Câu hỏi trong đề: Giải SGK Toán 9 CTST Bài tập cuối chương 5 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
b) Xét ∆ODE có OD = OE (cùng là bán kính của đường tròn (O) đường kính AB) nên ∆ODE cân tại O. Do đó đường cao OH đồng thời là đường trung tuyến của tam giác hay H là trung điểm của DE.
Xét tứ giác ADCE có hai đường chéo AC và DE cắt nhau tại trung điểm H của mỗi đường nên ADCE là hình bình hành.
Lại có DE ⊥ AC tại H nên hình bình hành ADCE là hình thoi.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi R là bán kính Trái Đất, khi đó R ≈ 6 400 km.
Đổi 65 m = 0,065 km; 5 m = 0,005 km.
Ta có: OA = R + 0,065 ≈ 6 400 + 0,065 = 6 400,065 (km).
OB = R + 0,005 ≈ 6 400 + 0,005 = 6 400,005 (km).
Xét ∆OHA vuông tại H, theo định lí Pythagore, ta có: OA2 = OH2 + AH2
Suy ra AH2 = OA2 – OH2 ≈ 6 400,0652 – 6 4002 = 832,004225.
Do đó
Xét ∆OHB vuông tại H, theo định lí Pythagore, ta có: OB2 = OH2 + BH2
Suy ra BH2 = OB2 – OH2 ≈ 6 400,0052 – 6 4002 = 64,000025.
Do đó
Ta có AB = AH + HB ≈ 28,84 + 8 = 36,84 (km).
Vậy với khoảng cách khoảng 36,84 kilômét thì người quan sát trên tàu bắt đầu trông thấy ngọn của hải đăng.
Lời giải
Đáp án đúng là: C
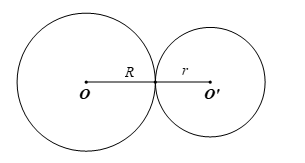
Ta có: 9 = 5 + 4 nên OO’ = R + r, suy ra hai đường tròn (O; 5 cm) và (O’; 4 cm) tiếp xúc ngoài.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
123 bài tập Nón trụ cầu và hình khối có lời giải
-
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đắk Lắk
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 01
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận