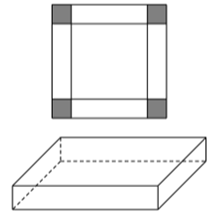
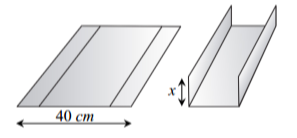
Bác Nam muốn uốn tấm tôn phẳng có dạng hình chữ nhật với bề ngang 40cm thành một rãnh dẫn nước bằng cách chia tấm tôn đó thành ba phần rồi gấp hai bên lại theo một góc vuông sao cho độ cao hai thành rãnh bằng nhau (hình bên). Để đảm bảo kĩ thuật, diện tích mặt cắt ngang của rãnh dẫn nước phải lớn lớn hoặc bằng 150cm2 Bác Nam cần làm rãnh dẫn nước có độ cao ít nhất là bao nhiêu cm?

Quảng cáo
Trả lời:
Khi chia tấm tôn đó thành ba phần rồi gấp hai bên lại theo một góc vuông như hình vẽ thì mặt cắt ngang là hình chữ nhật có hai kích thước \(x(\;{\rm{cm}})\) và \(40 - 2x(\;{\rm{cm}}).\)
Khi đó diện tích mặt cắt ngang là \(\left( {40 - 2x} \right)x\,\,\left( {\;{\rm{c}}{{\rm{m}}^2}} \right).\)
Ta thấy: Diện tích mặt cắt ngang của rãnh dẫn nước lớn hơn hoặc bằng \(150\;\,\,{\rm{c}}{{\rm{m}}^2}\) khi và chỉ khi
\(\left( {40 - 2x} \right)x \ge 150 \Leftrightarrow - 2{x^2} + 40x - 150 \ge 0.{\rm{ }}\)
Tam thức \(f(x) = - 2{x^2} + 40x - 150\) có hai nghiệm \({x_1} = 5,{x_2} = 15\) và hệ số \(a = - 2 < 0.\)
Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của \(x\) sao cho tam thức \(f\left( x \right)\) mang dấu "+" là khoảng \(\left( {5\,;\,\,15} \right).\)
Do đó tập nghiệm của bất phương trình \( - 2{x^2} + 40x - 150 \ge 0\) là đoạn \[\left[ {5\,;\,\,15} \right].\]
Vậy rãnh dẫn nước phải có độ cao ít nhất là \(5\,\;{\rm{cm}}.\)
Đáp án: 5.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
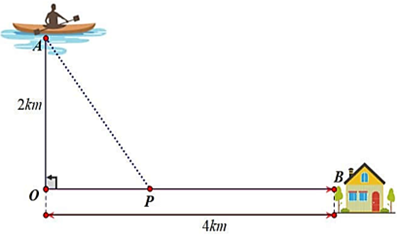
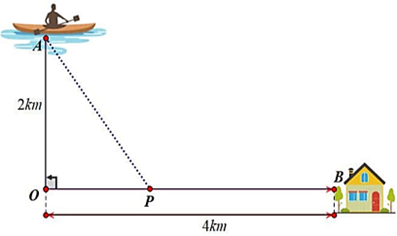
Đặt \(OP = x\,\,(0 < x < 4) \Rightarrow BP = 4 - x\,;\,\,AP = \sqrt {4 + {x^2}} .\)
Khoảng thời gian để anh Ba từ vị trí xuất phát đến được điểm \(B\) là:
\({t_{\left( x \right)}} = {t_{AP}} + {t_{PB}} = \frac{{\sqrt {4 + {x^2}} }}{6} + \frac{{4 - x}}{{10}}(h)\,\, \Rightarrow {t'_{\left( x \right)}} = \frac{x}{{6\sqrt {4 + {x^2}} }} - \frac{1}{{10}}.\)
\({t'_{\left( x \right)}} = 0 \Leftrightarrow \frac{x}{{6\sqrt {4 + {x^2}} }} - \frac{1}{{10}} = 0 \Leftrightarrow 3\sqrt {4 + {x^2}} = 5x \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{0 < x < 4}\\{4{x^2} = 9}\end{array} \Leftrightarrow x = \frac{3}{2}.} \right.\)
Bảng biến thiên:
|
\(x\) |
0 |
\(\frac{3}{2}\) |
4 |
|
\(t'\left( x \right)\) |
\( - \) |
0 + |
|
|
\(t\left( x \right)\) |
\(\frac{{11}}{{15}}\)
|
|
\(\frac{{\sqrt 5 }}{3}\)
|
|
|
|
\(\frac{2}{3}\) |
|
Từ bảng biến thiên suy ra khoảng thời gian ngắn nhất để anh Ba từ vị trí xuất phát đến được điểm \({\rm{B}}\) là: \({t_{\min }} = \frac{2}{3}(h) = \frac{2}{3}.60\) (phút) \( = 40\) (phút). Chọn A.
Lời giải
Gọi vị trí thấp nhất của ống bương là là vị trí của máng nước (như hình vẽ).
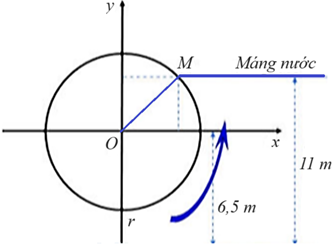
Tung độ của điểm \[M\] là \({y_M} = 11 - 6,5 = 4,5\)
\( \Rightarrow \sin \widehat {xOM} = \frac{{{y_M}}}{{OM}} = \frac{{4,5}}{5} = 0,9 \Rightarrow \widehat {xOM} \approx 64^\circ \).
Ta có \(\widehat {TOM} = \widehat {TOx} + \widehat {xOM} = 90^\circ + 64^\circ = 154^\circ .\)
Vì thời gian cọn nước thực hiện 1 vòng quay là 3 phút nên thời gian ống bương di chuyển từ \(T\)đến \(M\) là \(\frac{{3.154}}{{360}} = \frac{{77}}{{60}}\) (phút). Chọn C.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(x = 2.\)
B. \(x = 3.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.