Trong không gian với hệ trục tọa độ \[Oxyz,\] cho ba điểm \[A\left( {a\,;\,\,0\,;\,\,0} \right),\]\[\,\,B\left( {0\,;\,\,b\,;\,\,0} \right),\,\,\] \[C\left( {0\,;\,\,0\,;\,\,c} \right)\] với \(a,\,\,b,\,\,c > 0.\) Biết rằng \(\left( {ABC} \right)\) đi qua điểm \(M\left( {\frac{1}{7}\,;\,\,\frac{2}{7}\,;\,\,\frac{3}{7}} \right)\) và tiếp xúc với mặt cầu \(\left( S \right):{\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = \frac{{72}}{7}.\) Tính \(\frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}\).

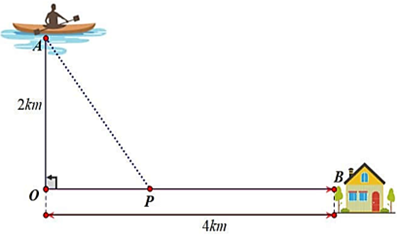
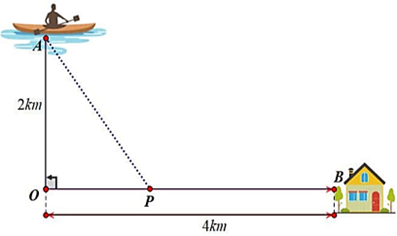
Đặt \(OP = x\,\,(0 < x < 4) \Rightarrow BP = 4 - x\,;\,\,AP = \sqrt {4 + {x^2}} .\)

Khoảng thời gian để anh Ba từ vị trí xuất phát đến được điểm \(B\) là:

\({t_{\left( x \right)}} = {t_{AP}} + {t_{PB}} = \frac{{\sqrt {4 + {x^2}} }}{6} + \frac{{4 - x}}{{10}}(h)\,\, \Rightarrow {t'_{\left( x \right)}} = \frac{x}{{6\sqrt {4 + {x^2}} }} - \frac{1}{{10}}.\)

\({t'_{\left( x \right)}} = 0 \Leftrightarrow \frac{x}{{6\sqrt {4 + {x^2}} }} - \frac{1}{{10}} = 0 \Leftrightarrow 3\sqrt {4 + {x^2}}  = 5x \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{0 < x < 4}\\{4{x^2} = 9}\end{array} \Leftrightarrow x = \frac{3}{2}.} \right.\)

Bảng biến thiên:

Từ bảng biến thiên suy ra khoảng thời gian ngắn nhất để anh Ba từ vị trí xuất phát đến được điểm \({\rm{B}}\) là: \({t_{\min }} = \frac{2}{3}(h) = \frac{2}{3}.60\) (phút) \( = 40\) (phút). Chọn A.

Gọi vị trí thấp nhất của ống bương là là vị trí của máng nước (như hình vẽ).

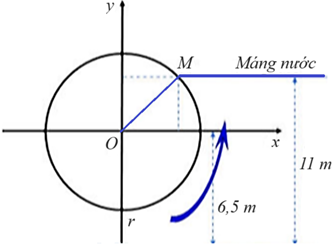
Tung độ của điểm \[M\] là \({y_M} = 11 - 6,5 = 4,5\)

\( \Rightarrow \sin \widehat {xOM} = \frac{{{y_M}}}{{OM}} = \frac{{4,5}}{5} = 0,9 \Rightarrow \widehat {xOM} \approx 64^\circ \).

Ta có \(\widehat {TOM} = \widehat {TOx} + \widehat {xOM} = 90^\circ  + 64^\circ  = 154^\circ .\)

Vì thời gian cọn nước thực hiện 1 vòng quay là 3 phút nên thời gian ống bương di chuyển từ \(T\)đến \(M\) là \(\frac{{3.154}}{{360}} = \frac{{77}}{{60}}\) (phút). Chọn C.