Cho parabol \(\left( {{P_1}} \right):y = - {x^2} + 2x + 3\) cắt trục hoành tại hai điểm \[A,\,\,B\] và đường thẳng \(d:y = a\,\,\left( {0 < a < 4} \right).\) Xét parabol \(\left( {{P_2}} \right)\) đi qua A, B và có đỉnh thuộc đường thẳng \(y = a.\) Gọi \({S_1}\) là diện tích hình phẳng giới hạn bởi \(\left( {{P_1}} \right)\) và \[d.\] Gọi \({S_2}\) là diện tích hình phẳng giới hạn bởi \(\left( {{P_2}} \right)\) và trục hoành. Biết \({S_1} = {S_2}\), tính \(T = {a^3} - 8{a^2} + 48a.\)
Quảng cáo
Trả lời:
Để việc tính toán trở nên đơn giản, ta tịnh tiến hai parabol sang trái một đơn vị.
Khi đó, phương trình các parabol mới là \(\left( {{P_1}} \right):y = - {x^2} + 4,\,\,\left( {{P_2}} \right):y = - \frac{a}{4}{x^2} + a.\)
Gọi \[A,\,\,B\] là các giao điểm của \(\left( {{P_1}} \right)\) và trục \(Ox \Rightarrow A\left( { - 2\,;\,\,0} \right),B\left( {2\,;\,\,0} \right) \Rightarrow AB = 4.\)
Gọi \[M,\,\,N\] là các giao điểm của \(\left( {{P_1}} \right)\) và đường thẳng \(d \Rightarrow M\left( { - \sqrt {4 - a} \,;\,a} \right),N\left( {\sqrt {4 - a} ;\,\,a} \right).\)
Ta có: \({S_1} = 2\int\limits_\alpha ^4 {\sqrt {4 - y} } dy = - \left. {\frac{4}{3}\left( {{{\left( {4 - y} \right)}^{\frac{3}{2}}}} \right)} \right|_\alpha ^4 = \frac{4}{3}\left( {4 - a} \right)\sqrt {4 - a} \);
\[{S_2} = 2\int\limits_\alpha ^2 {\left( { - \frac{a}{4}{x^2} + a} \right)} \,dx = \left. {2\left( { - \frac{{a{x^3}}}{{12}} + ax} \right)} \right|_0^2 = \frac{{8a}}{3}\].
Theo giả thiết \({S_1} = {S_2} \Rightarrow \frac{4}{3}\left( {4 - a} \right)\sqrt {4 - a} = \frac{{8a}}{3} \Leftrightarrow \left( {4 - {a^3}} \right) = 4{a^2} \Leftrightarrow {a^3} - 8{a^2} + 48a = 64\)
Vậy \(T = 64.\) Chọn B.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \(x\) (nghìn đồng) là giá phòng khách sạn sau khi tăng giá \((x > 400).\)
Giá chênh lệch sau khi tăng là: \(x - 400\) (nghìn đồng).
Số phòng trống lúc này là: \(2 \cdot \frac{{x - 400}}{{20}} = \frac{{x - 400}}{{10}}\) (phòng).
Số phòng cho thuê lúc này là: \(50 - \frac{{x - 400}}{{10}} = \frac{{900 - x}}{{10}}\) (phòng).
Số tiền phòng thu được là: \(f\left( x \right) = x \cdot \left( {\frac{{900 - x}}{{10}}} \right) = \frac{{ - {x^2} + 900x}}{{10}}\) (nghìn đồng).
Ta cần tìm \(x > 400\) sao cho \(f\left( x \right)\) đạt giá trị lớn nhất.
Dễ thấy \(x = - \frac{{900}}{{2 \cdot ( - 1)}} = 450\) thì lớn nhất. Đáp án: 450.
Câu 2
A. \(T = 6.\)
B. \(T = 0.\)
Lời giải
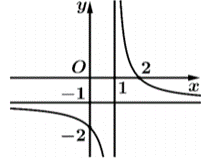
Từ đồ thị ta có:
• TCĐ: \(x = 1 \Rightarrow \frac{{ - d}}{{{c_a}}} = 1 \Rightarrow \frac{d}{c} = - 1 \Rightarrow d = - c\);
• TCN: \(y = - 1 \Rightarrow \frac{a}{c} = - 1 \Rightarrow a = - c\).
Đồ thị cắt trục hoành tại điểm: \(x = 2 \Rightarrow \frac{{ - b}}{a} = 2 \Rightarrow \frac{{ - b}}{{ - c}} = 2 \Rightarrow b = 2c\)
Vậy \(T = \frac{{a - 2b + 3d}}{c} = \frac{{ - c - 4c - 3c}}{c} = - 8\). Chọn C.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(4x - 3y + 18 = 0.\)
B. \(4x - 3y - 18 = 0.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.