Có 8 quyển sách Địa lí, 12 quyển sách Lịch sử, 10 quyển sách Giáo dục công dân (các quyển sách cùng một môn thì giống nhau) được chia thành 15 phần quả, mỗi phần gồm 2 quyển khác loại. Lấy ngẫu nhiên 2 phần quà từ 15 phần quà đó. Xác suất để hai phần quà lấy được khác nhau là
Quảng cáo
Trả lời:
Gọi số phần quà Sử - Địa là \[xx\], số phần quà Sử - GDCD là \[yy\] và số phần quà Địa - GDCD là \[zz.\]
Tổng số phần quà là 15 nên \(x + y + z = 15.\)
Phần quà có môn sử có 2 kiểu: Sử - Địa (\(x\) phần quà) và Sử - GDCD (\(y\) phần quà).
Do có 12 quyển sách sử nên 12 quyển này nằm hoàn toàn trong 2 kiểu phần quà trên.
Do đó: \(x + y = 12\).
Tương tự, ta có: Địa: \(z + x = 8;\) GDCD: \(y + z = 10.\)
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{x + y + z = 15}\\{x + y = 12}\\{y + z = 10}\\{x + z = 8}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 5}\\{y = 7}\\{z = 3}\end{array}} \right.} \right.\).
Suy ra số phần quà Sử - Địa là 5; Sử - GDCD là 7; Địa - GDCD là 3.
Chọn 2 trong 15 phần quà \( \Rightarrow \) Không gian mẫu \(n\left( \Omega \right) = C_{15}^2 = 105\).
Gọi A là biến cố: "Hai phần quà lấy được khác nhau", khi đó ta có:
\(n\left( A \right) = C_5^1 \cdot C_7^1 + C_7^1 \cdot C_3^1 + C_3^1 \cdot C_5^1 = 71\).
Vậy \[P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( P \right)}} = \frac{{71}}{{105}}.\] Chọn B.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \(x\) (nghìn đồng) là giá phòng khách sạn sau khi tăng giá \((x > 400).\)
Giá chênh lệch sau khi tăng là: \(x - 400\) (nghìn đồng).
Số phòng trống lúc này là: \(2 \cdot \frac{{x - 400}}{{20}} = \frac{{x - 400}}{{10}}\) (phòng).
Số phòng cho thuê lúc này là: \(50 - \frac{{x - 400}}{{10}} = \frac{{900 - x}}{{10}}\) (phòng).
Số tiền phòng thu được là: \(f\left( x \right) = x \cdot \left( {\frac{{900 - x}}{{10}}} \right) = \frac{{ - {x^2} + 900x}}{{10}}\) (nghìn đồng).
Ta cần tìm \(x > 400\) sao cho \(f\left( x \right)\) đạt giá trị lớn nhất.
Dễ thấy \(x = - \frac{{900}}{{2 \cdot ( - 1)}} = 450\) thì lớn nhất. Đáp án: 450.
Câu 2
A. \(T = 6.\)
B. \(T = 0.\)
Lời giải
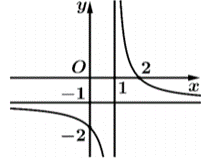
Từ đồ thị ta có:
• TCĐ: \(x = 1 \Rightarrow \frac{{ - d}}{{{c_a}}} = 1 \Rightarrow \frac{d}{c} = - 1 \Rightarrow d = - c\);
• TCN: \(y = - 1 \Rightarrow \frac{a}{c} = - 1 \Rightarrow a = - c\).
Đồ thị cắt trục hoành tại điểm: \(x = 2 \Rightarrow \frac{{ - b}}{a} = 2 \Rightarrow \frac{{ - b}}{{ - c}} = 2 \Rightarrow b = 2c\)
Vậy \(T = \frac{{a - 2b + 3d}}{c} = \frac{{ - c - 4c - 3c}}{c} = - 8\). Chọn C.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(4x - 3y + 18 = 0.\)
B. \(4x - 3y - 18 = 0.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.